Fisher's Blog

Sein heißt Werden
Leben heißt Lernen

0%

Deep Exploration via Bootstrapped DQN

发表于 更新于 分类于 阅读次数： Valine：

论文 Deep Exploration via Bootstrapped DQN 中，作者提出了一种 bootstrapped DQN 的探索方法，将深度探索与深度神经网络相结合，与一些抖动探索策略比如 ε-greedy 相比， 可以指数级地加快学习速度。

许多论文提出了一些理论上高效的深度探索方法，但绝大多数都是基于非常小的有限状态空间的 MDP 问题。另外还有一些论文比如著名的 Human-level control through deep reinforcement learning 采用的只是非常低效的探索方法或者根本不进行探索。

本文受 Thompson sampling （汤普森采样）的启发（通过随机选择最有可能是最优策略的策略来进行探索），提出了 bootstrapped DQN 探索方法。它可以显著地减少学习时间并且在大多数游戏中提高学习性能。

Posterior sampling in deep RL

Thompson sampling:

在多臂老虎机问题中，假设每个臂是否产生收益，其背后有一个概率分布，产生收益的概率为 \(p\) 。我们不断地试验，去估计出一个置信度较高的 概率 \(p\) 的概率分布 就能近似解决这个问题了。

怎么能估计概率p的概率分布呢？ 答案是假设概率p的概率分布符合 Beta(win, lose) 分布，它有两个参数: win, lose。

每个臂都维护一个 Beta 分布的参数。每次试验后，选中一个臂，摇一下，有收益则该臂的 win 增加 1，否则该臂的 lose 增加 1。

每次选择臂的方式是：用每个臂现有的 Beta 分布产生一个随机数 b，选择所有臂产生的随机数中最大的那个臂去摇。

1
choice = numpy.argmax(pymc.rbeta(1 + self.wins, 1 + self.trials - self.wins))

数学形式可以写为： \[ \begin{align*} &\theta_1,\cdots,\theta_n \sim \hat{p}(\theta_1,\cdots,\theta_n) \\ &a=\arg\max_a E_{\theta_a}[r(a)] \end{align*} \]

类比于 MDP 中的 \(Q\) 函数：

  1. 从 \(Q\) 函数的分布 \(p(Q)\) 中采样得到 \(Q\)
  2. 根据采样得到的 \(Q\) 函数采取一步行动
  3. 更新 \(p(Q)\) ，并不断重复上述 1-3 步

Bootstrap

设总体的分布 \(F\) 未知，但已经有一个容量为 \(n\) 的来自分布 \(F\) 的数据样本 \(\mathcal{D}\) 。自这一样本按放回抽样的方法抽样 \(N\) 次，得到 \(\mathcal{D}_1,\cdots,\mathcal{D}_N\) ，每一个样本集 \(\mathcal{D}_i\) 的容量为 \(n\) 。利用这些样本对总体 \(F\) 进行统计推断，这种方法称为 bootstrap （自助法）。我们通过每个样本集 \(\mathcal{D}_i\) 训练模型 \(f_{\theta_i}\) ，为了达到从 \(p(\theta)\) 采样的效果，我们用 \(f_{\theta_i}\) 进行采样 \(i\in[1,\cdots,N]\)

但要训练 \(N\) 个独立的神经网络的代价太高了，论文中设计了下图所示的网络结构：

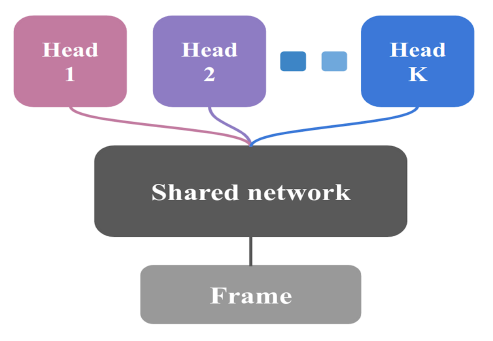
只用一个网络，但是并行地输出为 K 个不同的 head 代替原来 K 个不同的神经网络输出。

Bootstrapped DQN

先回顾一下 Double DQN： \[ \theta_{t+1}\leftarrow\theta_t+\alpha(y_t^Q-Q(s_t,a_t;\theta_t)) \nabla_\theta Q(s_t,a_t;\theta_t) \] 其中： \[ y_t^Q\leftarrow r_t+\gamma \max_a Q(s_{t+1},\arg\max_a Q(s_{t+1},a;\theta_t);\theta^-) \] Bootstrapped DQN 将传统 DQN 修改了一下，通过 bootstrap 方法来估计 \(Q\) 函数的分布。在每个回合的一开始，bootstrapped DQN 采样一个 \(Q\) 函数，智能体接下去会将这个 \(Q\) 函数视为这个回合最优的策略。

具体算法如下：

其中 \(Q_k\) 表示第 \(k\) 个网络输出的 head。在 bootstrapped DQN 中非常重要的一个思想是 bootstrap mask \(m_t\) ，\(m_t\) 决定了在 \(t\) 时刻生成的经验 \((s_t,a_t,r_{t+1},s_{t+1},m_t)\) 可以被哪几个 \(Q\) 函数所学习。\(m_t\) 最简单的形式就是长度为 \(K\) 的二进制数组。\(M\) 分布负责生成每一个 \(m_t\) 比如 \(M\) 可以类似伯努利分布以每个 head 为 0.5 概率生成 \(m_t\) ，或者全部为 1，也可以 \(M_t[k]\sim Poi(1)\) 或 \(M_t[k]\sim \text{Exp}(1)\) 。对于第 \(t\) 个在经验池中的经验元组来说，梯度 \(g_t^k\) 为 \[ g_t^k=m_t^k(y_t^Q-Q_k(s_t,a_t;\theta))\nabla_\theta Q_k(s_t,a_t;\theta) \]

在伯克利的深度强化学习课程中，举了一个潜艇游戏的例子。如果以随机的行为（比如 ε-greedy）进行探索的话，潜艇会前后摆动，不大可能进入一些有趣的地方。而使用随机的 \(Q\) 函数进行探索，尽管看上去是随机的，但对于整个回合来说，内在还是一个一致的策略。

参考

Osband, I., Blundell, C., Pritzel, A., & Van Roy, B. (2016). Deep exploration via bootstrapped DQN. In Advances in neural information processing systems (pp. 4026-4034).

https://zhuanlan.zhihu.com/p/21388070

盛骤. (2001). 概率论与数理统计:第三版. 高等教育出版社.