Adapting Auxiliary Losses Using Gradient Similarity & Adaptive Auxiliary Task Weighting for Reinforcement Learning

在强化学习中， 一直存在数据利用率低的问题，尤其是在观测值是高维图像的情况下。如果引入一些额外的辅助任务，将这些任务的知识迁移到强化学习主任务中是一个可以提高数据利用率的方法，同时也能帮助提高强化学习的基础表征，但如何将这些辅助任务进行融合是一个大问题，因为不确定这些辅助任务是否真的在帮助主任务，也不知道它们何时会对主任务的训练产生反作用。

Adapting Auxiliary Losses Using Gradient Similarity & Adaptive Auxiliary Task 主要利用各任务梯度之间的余弦相似度作为权重来判断辅助任务是否在帮助降低主任务的损失。Adaptive Auxiliary Task Weighting for Reinforcement Learning 则提出了一种在线学习的算法，主要基于辅助任务应该从长远来看提供一种帮助降低主任务损失的梯度方向。两篇论文都是想要动态调节辅助任务损失的权重来达到融合辅助任务的作用。

Adapting Auxiliary Losses Using Gradient Similarity

问题定义

假设我们有一个主任务 \(\mathcal{T}_{main}\) 和一个辅助任务 \(\mathcal{T}_{aux}\) ，并分别有两个损失 \(\mathcal{L}_{main}\) 和 \(\mathcal{L}_{aux}\) 。我们其实只关心优化任务 \(\mathcal{T}_{main}\) ，对于辅助任务我们并不直接关心。作者的目标就是要能设计一种算法能够：

1. 在辅助任务确实能够提供帮助的时候利用辅助任务，也就是学习地更快
2. 当辅助任务不提供帮助的时候阻断辅助任务的影响，也就是只依靠主任务来进行训练。

需要注意的是，这与多目标学习不同，因为并不是要同时学习好两种任务，主要目标还是学习好主任务，辅助任务只是起到辅助作用。

我们将 \(\mathcal{T}_{main}\) 和 \(\mathcal{T}_{aux}\) 参数化为两个神经网络 \(f(\cdot,\theta,\phi_{main})\) 和 \(g(\cdot,\theta,\phi_{aux})\) ，他们共享参数 \(\theta\) 。一般来说，辅助任务的损失尽量最小化 \[ \underset{\boldsymbol{\theta}, \boldsymbol{\phi}_{\operatorname{main}}, \boldsymbol{\phi}_{a u x}}{\arg \min } \mathcal{L}_{\operatorname{main}}\left(\boldsymbol{\theta}, \boldsymbol{\phi}_{\text {main}}\right)+\lambda \mathcal{L}_{a u x}\left(\boldsymbol{\theta}, \boldsymbol{\phi}_{a u x}\right) \tag{1} \] 因为从直觉上来说，如果两种任务是有关联的话，通过优化 \(\theta\) 而最小化 \(\mathcal{L}_{aux}\) 可以帮助最小化 \(\mathcal{L}_{main}\) 。作者将 \(\lambda\) 建模为在每一个训练迭代时刻 \(t\) ，给定 \(\theta^{(t)}, \phi_{main}^{(t)}, \phi_{aux}^{(t)}\) ，任务 \(\mathcal{T}_{aux}\) 对 \(\mathcal{T}_{main}\) 有多大帮助，即我们希望 \[ \underset{\lambda^{(t)}}{\arg \min } \mathcal{L}_{\operatorname{main}}\left(\boldsymbol{\theta}^{(t)}-\alpha \nabla_{\boldsymbol{\theta}}\left(\mathcal{L}_{\text {main}}+\lambda^{(t)} \mathcal{L}_{\text {aux}}\right), \boldsymbol{\phi}_{\text {main}}^{(t)}-\alpha \nabla_{\boldsymbol{\phi}_{\text {main}}} \mathcal{L}_{\text {main}}\right) \tag{2} \] 而要解决公式 (2) 非常困难，作者换了一种启发式的方法，比将 \(\lambda\) 作为一个常量固定更好，同时也不需要调参。

任务梯度之间的余弦相似度 (Cosine Similarity Between Gradients Of Tasks)

作者利用任务梯度之间的余弦相似度来衡量任务之间的相似度，并以此估计 \(\lambda^{(t)}\) 。

举个例子，如果主任务是最小化 \(\mathcal{L}_{\text {main}}=(\theta-10)^{2}\) ，辅助任务是 \(\mathcal{L}_{a u x}=\theta^{2}\) ，它们的梯度为 \(\nabla_{\theta} \mathcal{L}_{\text {main}}=2(\theta-10)\) 和 \(\nabla_{\theta} \mathcal{L}_{a u x}=2 \theta\) 。当 \(\theta\) 初始化为 \(\theta=-20\) ，两种任务的梯度方向相同，余弦相似度为 1，此时最小化辅助任务损失有助于最小化主任务。但如果在 \(\theta=5\) 这个点，两种任务的梯度就是相反的，余弦相似度为 -1，此时最小化辅助任务损失会阻碍最小化主任务损失。下图描述了整个过程。

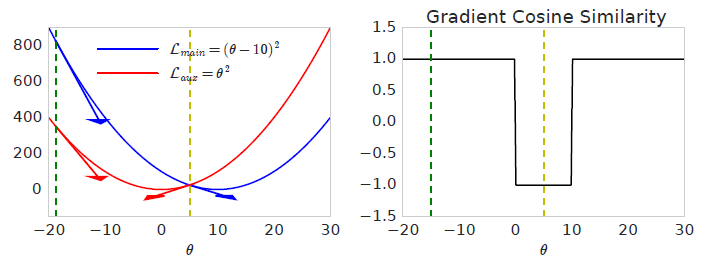
以此可以自然而然引出一种策略：当辅助损失梯度与主损失梯度的余弦相似度非负时最小化辅助损失，否则忽略辅助损失梯度。即可以有如下命题：

给定任意的梯度向量 \(G(\boldsymbol{\theta})=\nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})\) 和任意向量 \(V(\boldsymbol{\theta})\) （如另一种任务的损失或其他任意向量），参数更新形式 \[ \boldsymbol{\theta}^{(t+1)}:=\boldsymbol{\theta}^{(t)}-\alpha^{(t)}\left(G\left(\boldsymbol{\theta}^{(t)}\right)+V\left(\boldsymbol{\theta}^{(t)}\right) \max \left(0, \cos \left(G\left(\boldsymbol{\theta}^{(t)}\right), V\left(\boldsymbol{\theta}^{(t)}\right)\right)\right)\right. \] 可以收敛到 \(\mathcal{L}\) 的局部最优点上。

注意以上命题不能保证对收敛性有提升作用，只能保证减少发散的可能。

上述命题假设所有损失具有相同的参数 \(\theta\) ，但公式 (2) 假设每种任务还有独有的参数 \(\phi_{main}, \phi_{aux}\) ，所以需要以下命题：

给定参数为 \(\Theta\) 的两种损失（某些参数为共享参数 \(\theta\) ，某些为独有参数 \(\phi_{main}, \phi_{aux}\)），参数更新形式 \[ \begin{align*} \boldsymbol{\theta}^{(t+1)} &:= \boldsymbol{\theta}^{(t)}-\alpha^{(t)}\bigg(\nabla_{\boldsymbol{\theta}} \mathcal{L}_{\operatorname{main}}\left(\boldsymbol{\theta}^{(t)}\right)+\nabla_{\boldsymbol{\theta}} \mathcal{L}_{a u x}\left(\boldsymbol{\theta}^{(t)}\right) { \color{red}\max \Big( 0, \cos \left(\nabla_{\boldsymbol{\theta}} \mathcal{L}_{\operatorname{main}}\left(\boldsymbol{\theta}^{(t)}\right), \nabla_{\boldsymbol{\theta}} \mathcal{L}_{a u x}\left(\boldsymbol{\theta}^{(t)}\right)\right)\Big) } \bigg) \\ \phi_{\text {main}}^{(t+1)} &:= \phi_{\text {main}}^{(t)}-\alpha^{(t)} \nabla_{\boldsymbol{\phi}_{\text {main}}} \mathcal{L}_{\operatorname{main}}\left(\boldsymbol{\Theta}^{(t)}\right) \quad \text { and } \quad \boldsymbol{\phi}_{a u x}^{(t+1)}:=\boldsymbol{\phi}_{a u x}^{(t)}-\alpha^{(t)} \nabla_{\boldsymbol{\phi}_{a u x}} \mathcal{L}_{a u x}\left(\boldsymbol{\Theta}^{(t)}\right) \end{align*} \] 可以收敛到 \(\mathcal{L}_{main}\) 的局部最优点上。

与第一个命题先比较，即将 \(G=\nabla_{\boldsymbol{\theta}} \mathcal{L}_{\text {main}}\) ， \(V=\nabla_{\boldsymbol{\theta}} \mathcal{L}_{a u x}\) 。

对于算法的无权重版本该命题依然成立，我们可以不以 \(\cos(G,V)\) 作为权重，而是用二值权重 \((\text{sign}(\cos(G,V))+1)/2\) ，即当 \(\cos(G,V)>0\) 时使用 \(V\) 。

Adaptive Auxiliary Task Weighting for Reinforcement Learning

问题定义

这篇论文的符号使用与前文比较类似，假设有一个主任务 \(\mathcal{T}_{main}\) 和一系列辅助任务 \(\mathcal{T}_{aux,i}\) ，其中 \(i\in \{1,2,\cdots,K\}\) ，并分别对应损失 \(\mathcal{L}_{main}\) 和 \(\mathcal{L}_{aux,i}\) 。将主任务与辅助任务损失融合后变成： \[ \mathcal{L}\left(\theta_{t}\right)=\mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right)+\sum_{i=1}^{K} w_{i} \mathcal{L}_{a u x, i}\left(\theta_{t}\right) \] 即辅助任务损失前加了权重 \(w_i\) ，模型参数更新公式为： \[ \theta_{t+1}=\theta_{t}-\alpha \nabla_{\theta_{t}} \mathcal{L}\left(\theta_{t}\right) \]

Local Update from One-step Gradient

我们首先去寻找能使主任务损失下降的最快的辅助权重。定义 \(\mathcal{V}_t(\boldsymbol{w})\) 为主任务损失在 \(t\) 时刻下降的速度，其中 \(\boldsymbol{w}=[w_1, \cdots, w_k]^{T}\) ，可以有： \[ \begin{aligned} \mathcal{V}_{t}(\boldsymbol{w})=\frac{d \mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right)}{d t} & \approx \mathcal{L}_{\operatorname{main}}\left(\theta_{t+1}\right)-\mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right) \\ &=\mathcal{L}_{\operatorname{main}}\left(\theta_{t}-\alpha \nabla_{\theta_{t}} \mathcal{L}\left(\theta_{t}\right)\right)-\mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right) \\ & \approx \mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right)-\alpha \nabla_{\theta_{t}} \mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right)^{T} \nabla_{\theta_{t}} \mathcal{L}\left(\theta_{t}\right)-\mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right) \\ &=-\alpha \nabla_{\theta_{t}} \mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right)^{T} \nabla_{\theta_{t}} \mathcal{L}\left(\theta_{t}\right) \end{aligned} \tag{3} \] \(\alpha\) 是梯度步长。第一行公式是从时间导数的有限差分近似中获得的，即 \(\Delta t=1\) ，第三行公式是一阶泰勒近似。

要更新 \(\boldsymbol{w}\) ，我们可以简单地计算它的梯度： \[ \frac{\partial \mathcal{V}_{t}\left(w_{i}\right)}{\partial w_{i}}=-\alpha \nabla_{\theta_{t}} \mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right)^{T} \nabla_{\theta_{t}} \mathcal{L}_{a u x, i}\left(\theta_{t}\right), \forall i=1, \ldots, K \tag{4} \] 实际上就是主任务损失梯度与辅助任务损失梯度的点积。从直观上来讲，这个方法利用了在线更新过程中经验来判断辅助任务是否真的在帮助降低主任务损失。这就很想上文的余弦相似度方法来判断是否要去用某个辅助任务，但是此更新公式是基于最大化主任务损失下降速度，实验证明这个方法比用余弦近似会更好。

N-step Update

公式 4 的的梯度实际上是公式 3 中的顺时更新 \(d \mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right) / dt\) ，但我们不仅仅需要关注 one-step 的主任务损失更新，更应该关注主任务损失在多步之后的长远更新。所以我们现在优化主任务损失的 N-step 下降速度： \[ \mathcal{V}_{t}^{N}(\boldsymbol{w})=\mathcal{L}_{\operatorname{main}}\left(\theta_{t+N}\right)-\mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right) \] 要计算上式关于 \(\boldsymbol{w}\) 的梯度需要计算高阶雅各比矩阵，这非常消耗计算性能，所以作者只计算了一阶近似： \[ \begin{aligned} \mathcal{V}_{t}^{N}(\boldsymbol{w}) & \doteq \mathcal{L}_{\operatorname{main}}\left(\theta_{t+N}\right)-\mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right) \\ &=\mathcal{L}_{\operatorname{main}}\left(\theta_{t+N-1}-\alpha \nabla_{\theta_{t+N-1}} \mathcal{L}\left(\theta_{t+N-1}\right)\right)-\mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right) \\ & \approx \mathcal{L}_{\operatorname{main}}\left(\theta_{t+N-1}\right)-\mathcal{L}_{\operatorname{main}}\left(\theta_{t}\right)-\alpha \nabla_{\theta_{t+N-1}} \mathcal{L}_{\operatorname{main}}\left(\theta_{t+N-1}\right)^{T} \nabla_{\theta_{t+N-1}} \mathcal{L}\left(\theta_{t+N-1}\right) \\ & \vdots \\ & \approx-\alpha \sum_{j=0}^{N-1} \nabla_{\theta_{t+j}} \mathcal{L}_{\operatorname{main}}\left(\theta_{t+j}\right)^{T} \nabla_{\theta_{t+j}} \mathcal{L}\left(\theta_{t+j}\right) \end{aligned} \] 省略了其它高阶项后，一阶的梯度近似为： \[ \nabla_{w_{i}} \mathcal{V}_{t}^{N}\left(w_{i}\right) \approx-\alpha \sum_{j=0}^{N-1} \nabla_{\theta_{t+j}} \mathcal{L}_{\operatorname{main}}\left(\theta_{t+j}\right)^{T} \nabla_{\theta_{t+j}} \mathcal{L}_{a u x, i}\left(\theta_{t+j}\right) \tag{6} \] 每个都是一个标量，更新权重 \(w_i\) 。论文中，这个更新方式称之为 Online Learning for Auxiliary losses (OL-AUX) 。在实际中，为了平衡多个损失的梯度，作者使用了 Adaptive Loss Balancing 方法，即将所有辅助任务的损失都套了一个 log。下列展示了此算法：

每 \(N\) 次更新，就应用公式 6 更新权重。

作者在实验部分尝试了五种辅助任务：

1. Forward Dynamics，给定当前时刻的观测值和动作，预测下一时刻的观测值的隐状态；
2. Inverse Dynamics，给定连续的观测值，预测所执行的动作；
3. Egomotion，给定原始图像和变换过后的图像，预测变换的方式；
4. Autoencoder，从隐状态重建原始观测值；
5. Optical Flow，给定连续的图像观测值，预测光流。

参考

Du, Y., Czarnecki, W. M., Jayakumar, S. M., Pascanu, R., & Lakshminarayanan, B. (2018). Adapting auxiliary losses using gradient similarity. arXiv preprint arXiv:1812.02224.

Lin, X., Baweja, H., Kantor, G., & Held, D. (2019). Adaptive Auxiliary Task Weighting for Reinforcement Learning. In Advances in Neural Information Processing Systems (pp. 4772-4783).