本文翻译自 Understanding Variational Autoencoders (VAEs), Joseph Rocca, Sep 24, 2019
这篇文章里,我们主要介绍一种深度生成模型:Variational Autoencoders (VAEs)。概括地说,VAE 就是一个自动编码器(autoencoder),但它编码后的分布在训练阶段需要被正则化,以此让它的隐空间(latent space)有足够好的性质来使我们生成新的数据。另外,用 variational 这个词是因为该方法与正则化和统计学中的变分推断有关。
降维,PCA 与 autoencoders
在这一小节,我们讨论与降维有关的一些符号定义,同时简要回顾下主成分分析(PCA)和 autoencoders,并说明这个两个方法其实是有关联的。
什么是降维?
在机器学习中,降维就是减少描述某些数据的特征数量(dimensionality reduction is the process of reducing the number of features that describe some data)。这个减少的过程要么就是选择(selection,只有一部分已存在的特征被保留下来),要么就是抽取(extraction,从原有的特征中生成数量较少的新特征)。降维可以用在许多需要低维度数据的领域中(数据可视化、数据储存、运算量大的计算等)。尽管有许多不同的方法可以做到降维,我们可以设置一个与这些方法中的大多数相匹配的通用框架。
首先,我先将 encoder 当作使一种从“旧特征”产生“新特征”的过程,decoder 是这一过程的反过程。降维相当于是数据的压缩,encoder 压缩数据(从原始特征空间到编码空间,也叫隐空间 latent space),decoder 解压。当然根据初始数据分布、隐空间的维度还有 encoder 的定义,这个压缩过程也能是有损的,也就意味着一部分信息在 encoding 过程中可能会丢失,decoding 过程无法还原这些特征。
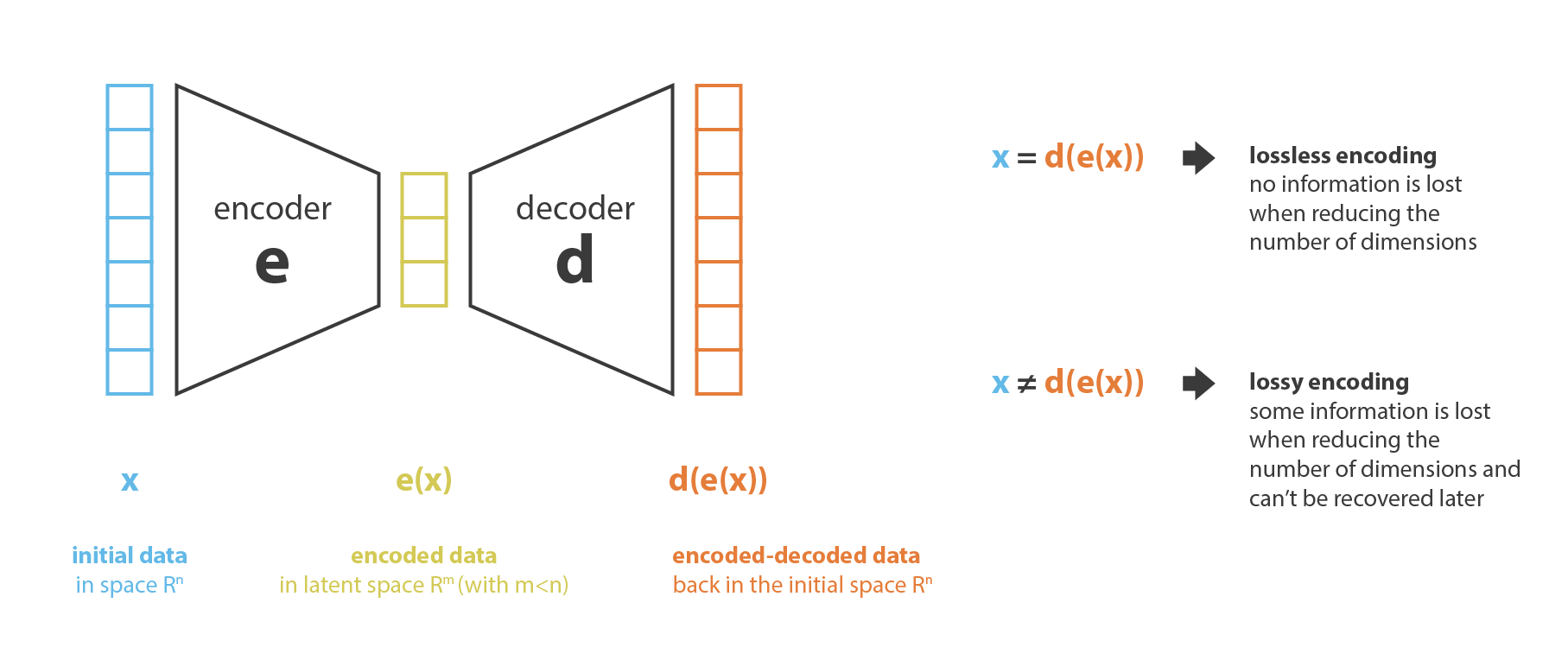
降维做主要的目的就是找到一组最佳的 encoder, decoder,换句话说,给定一系列可能的 encoder, decoder,我们就是要找到能保留最多信息的 encoder 和能产生最少重建误差(reconstruction error)的 decoder。如果我们分别用 \(E\) 和 \(D\) 来表示所有可能的 encoder 和 decoder,那么降维问题可以写成: \[ \left(e^{*}, d^{*}\right)=\underset{(e, d) \in E \times D}{\arg \min } \epsilon(x, d(e(x))) \] 其中 \(\epsilon(x, d(e(x)))\) 定义了输入 \(x\) 与 encode, decode 后 \(d(e(x))\) 之间的重建误差(reconstruction error)。接下来我们用 \(N\) 表示数据的个数,\(n_d\) 表示原始数据的空间维度,也就是 decoded 的空间维度,\(n_e\) 表示降维后的空间维度(encoded)。
Principal components analysis (PCA)
一说到降维,第一个想到的应该就是 PCA 了,为了能用我们之前提到的通用框架来解释,同时也为了引出 autoencoders,我们简要回顾下 PCA。
PCA 就是想要以线性组合的方式,从 \(n_d\) 个原始特征,构建 \(n_e\) 个互相独立的新特征,以此让原始数据在子空间上的映射与原始数据之间尽可能接近。换句话说,PCA 就是要去找一个最好的相对于原始空间的子空间(新特征的正交基),来让原始数据在这个子空间上的投影近似误差越小越好。
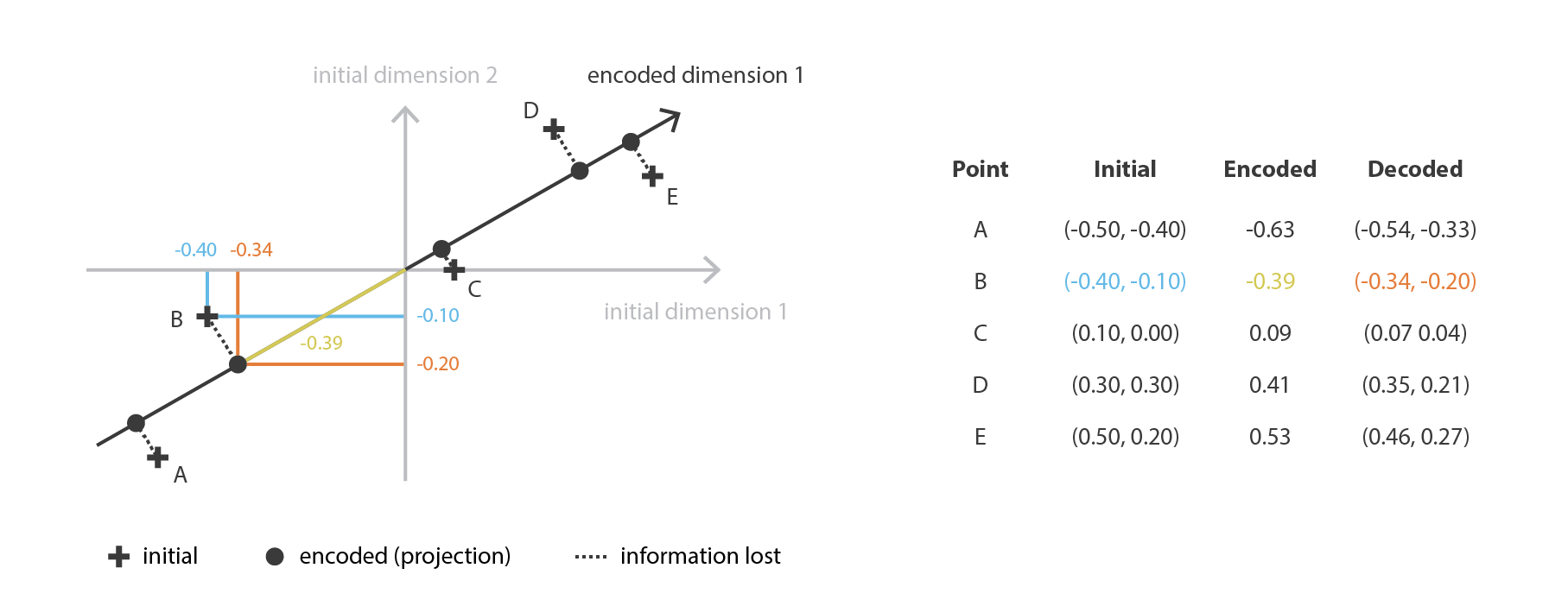
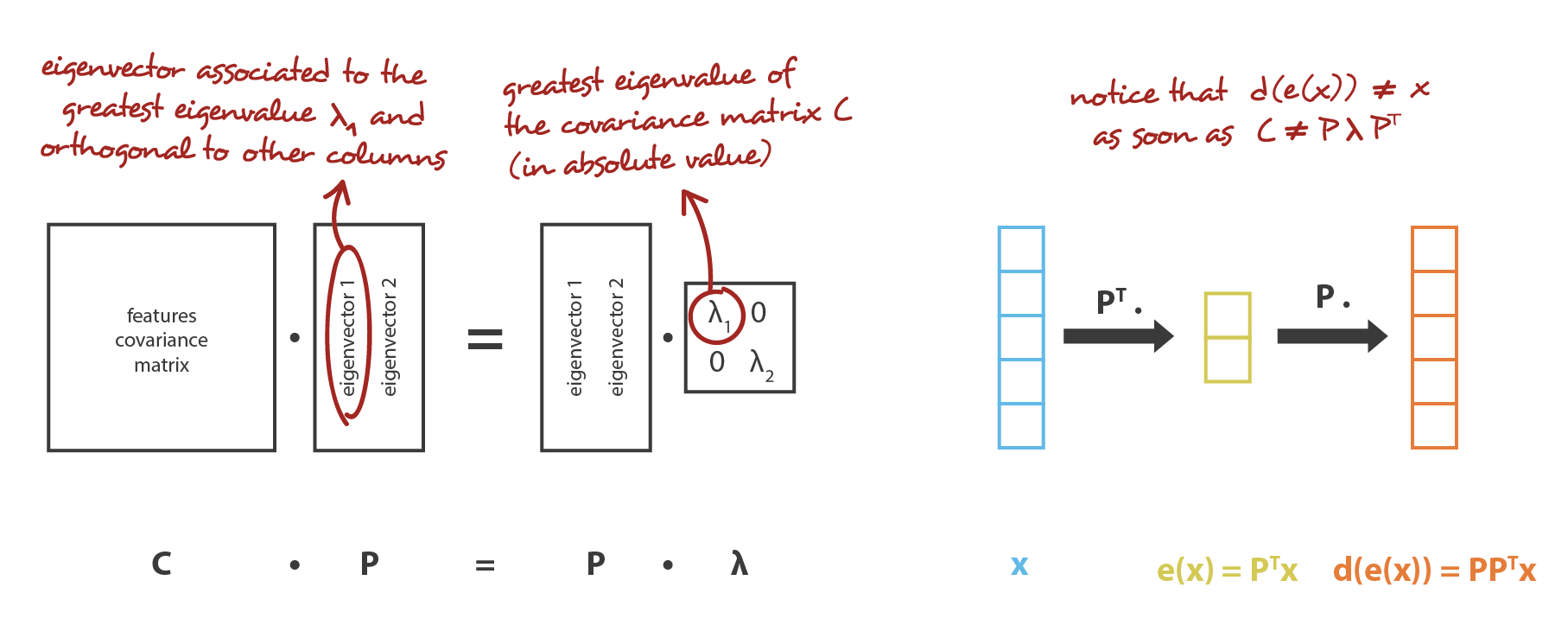
如果用我们的框架来解释的话,就是我们要在一堆行是标准正交化的 \(n_d \times n_e\) 矩阵 \(E\) 中要到一个 encoder,同时要在一堆 \(n_e \times n_d\) 矩阵 \(D\) 中找到对应的 decoder。可以证明,与协方差特征矩阵的 \(n_e\) 个最大特征值相对应的特征向量是正交的,并定义维度为 \(n_e\) 的最佳子空间有着最小的投影数据近似误差。 因此,可以将这些 \(n_e\) 个特征向量选择为我们的新特征,因此,降维问题可以表示为特征值、特征向量问题。 此外,在这种情况下,decoder 矩阵就是 encoder 矩阵的转置。
Autoencoders
现在,我们讨论 autoencoders,来看如何使用神经网络来降低维度。autoencoders 的总体思路非常简单,包括将 encoder 和 decoder 设置为神经网络,并使用迭代优化来学习最佳的 encoding-decoding 方案。因此,在每次迭代中,我们向 autoencoders 提供一些数据,我们将 encoded-decoded 后的输出与初始数据进行比较,并将误差通过 autoencoders 反向传播以更新审京网络的权重。
因此,直观地讲,整个 autoencoders 架构(encoder + decoder)会造成一个数据的瓶颈,从而确保只有信息的主要部分可以通过 autoencoders 并进行重构。从我们的通用框架角度来看, encoder 的神经网络结构定义了一系列的 encoders \(E\) ,同理 decoder 的神经网络结构定义了一系列的 decoders \(D\) ,通过最小化梯度下降这些网络的参数来完成对 encoder 和 decoder 的搜索,以最大程度地减少重构误差。
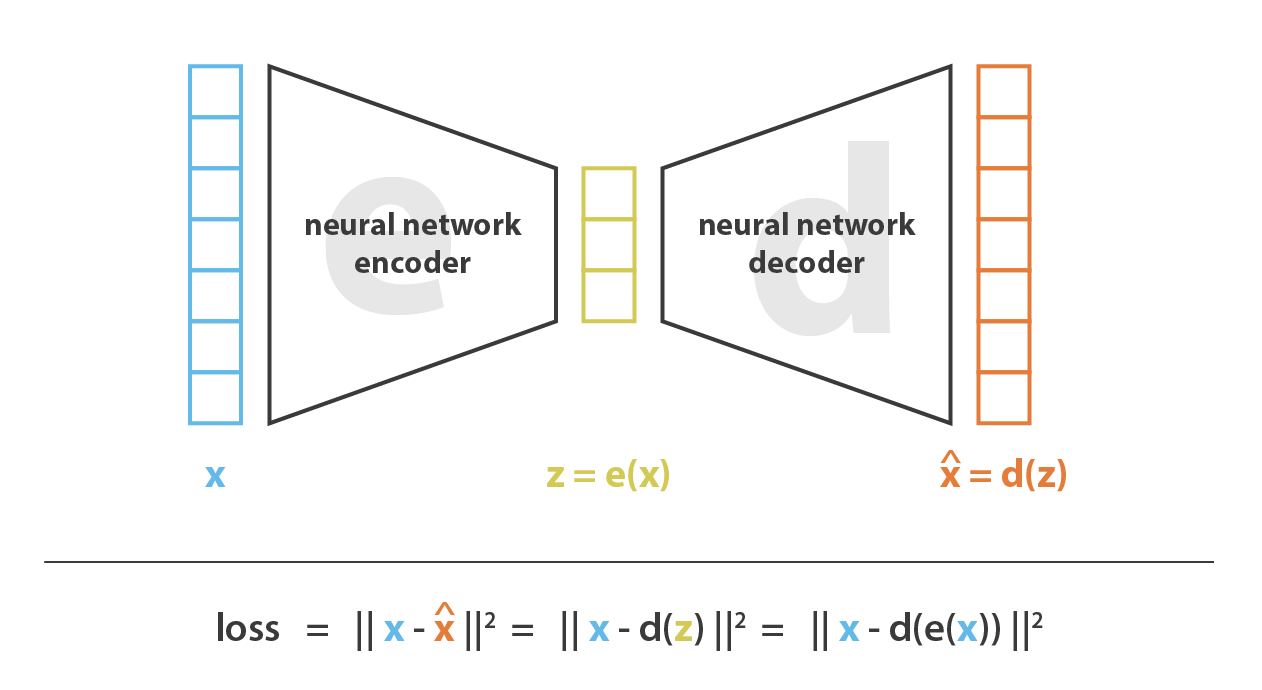
首先,假设我们的 encoder, decoder 的网络架构都只有一层,也没有用到非线性的激活器(线性 autoencoder)。 这样的 encoder 和 decoder 就是简单的线性变换,可以表示为矩阵。 在这种情况下,在某种意义上,我们可以看到与 PCA 的关系,就像 PCA 一样,我们就是要去找最佳的线性子空间来投影数据,而这样做时要尽可能减少信息丢失。 用 PCA 获得的 encoder,decoder 矩阵自然定义了用梯度下降算法所能满足的一种解决方案,但这不是唯一的解决方案。 事实上,某些基向量可以来描述相同的最佳子空间,因此,几个 encoder对也可以给出最佳的重构误差。 此外,对于线性 autoencoder(与PCA相反),我们最终获得的新特征不一定是独立的(神经网络中没有正交性约束)。
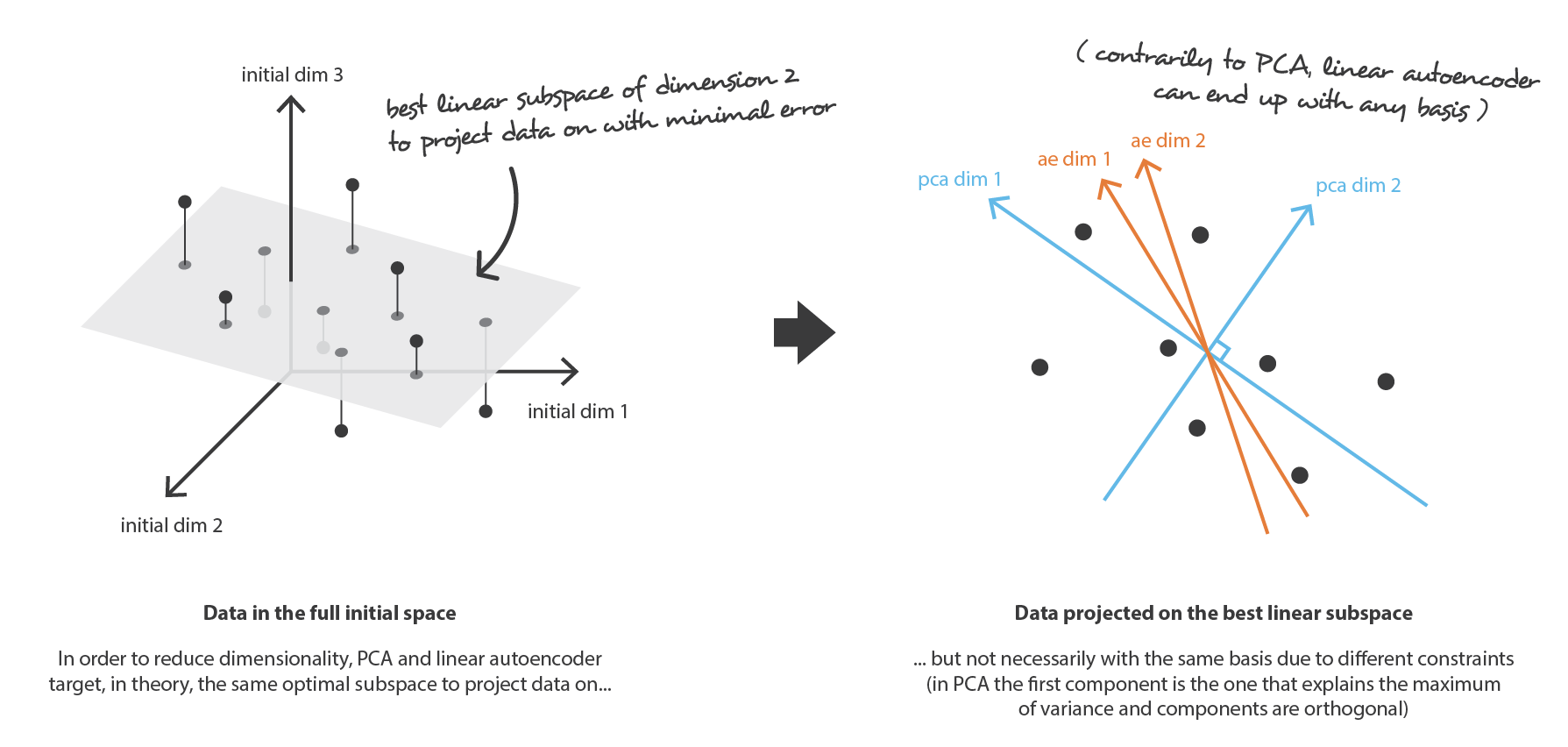
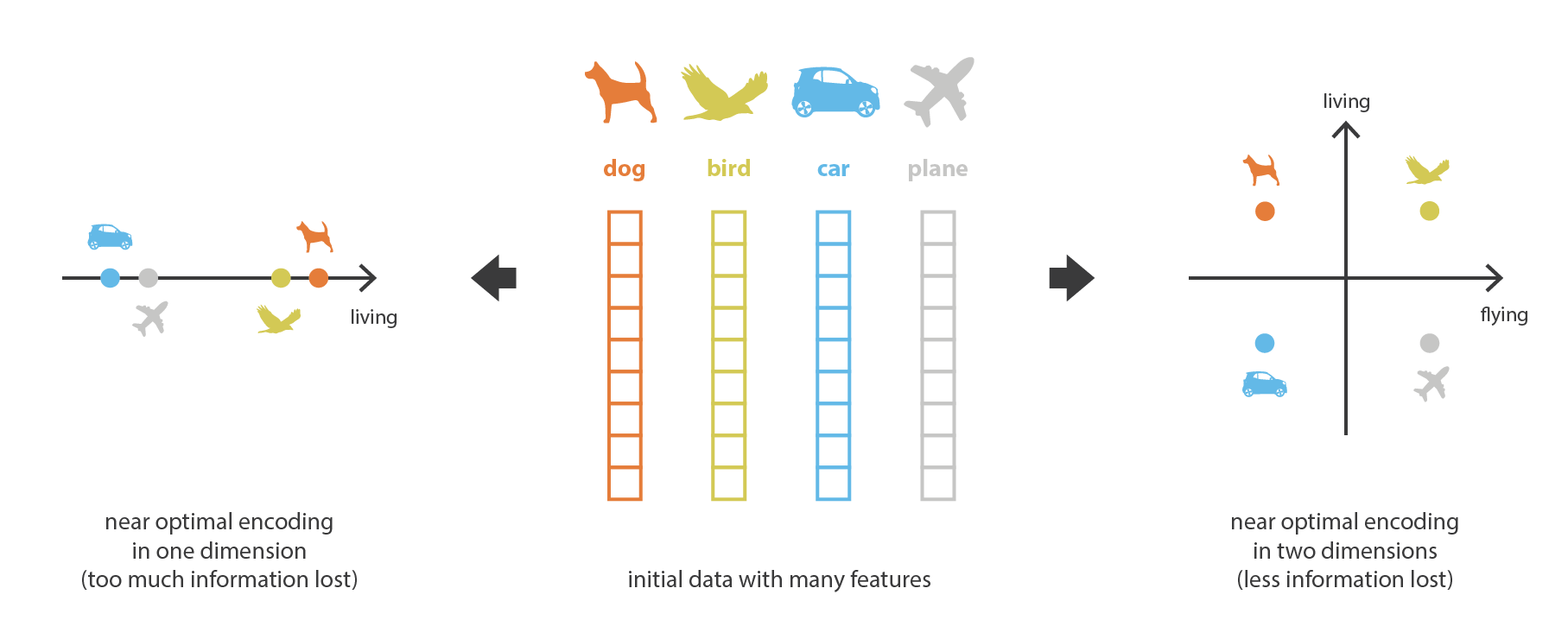
现在,假设 encoder 和 decoder 都是深度的且非线性的。 在这种情况下,网络结构越复杂,autoencoder 越可以降低更多的维度,同时保持较低的重构损失。 直观地讲,如果我们的 encoder 和 decoder 具有足够的自由度,则可以将任何初始维数减小为 1。也确实,具有“无限能力”的 encoder 理论上可以将我们的 N 个初始数据编码为1、2、3,……N 个,并且对应的 decoder 也可以进行逆变换,而在此过程中不会造成任何损失。
但是,在我们应该注意两点。 首先,没有重建损失的降维通常要付出代价:隐空间中缺乏可解释和可利用的结构(缺乏正则化),其次,在大多数情况下,降维的最终目的不仅仅是减少数据的维数,而且要在减少维数的同时将数据结构信息的主要部分保留在简化的表征中。 由于这两个原因,必须根据降维的最终目的来仔细控制和调整隐空间的尺寸和 autoencoder 的“深度”(压缩的程度和质量)。
Variational Autoencoders
到目前为止,我们已经讨论了降维问题,并介绍了 autoencoders,它们是可以通过梯度下降训练的 encoder-decoder 架构。 现在,让我们联系样本生成问题,看看当前 autoencoders 的限制,并介绍 variational autoencoders。
Autoencoders 在样本生成中的限制
现在,自然会想到一个问题:“autoencoders 和样本生成之间的联系是什么?”。 确实,一旦对 autoencoders 进行了训练,我们既有 encoder 又有 decoder,但仍然没有一种方式来产生任何新内容。 乍一看,我们可能会认为,如果隐空间足够正则化(在训练过程中 encoder 很好地“组织”了),我们可以从该隐空间中随机取一个点并 decode 以得到一个新的样本,然后,decoder 将或多或少像生成对抗网络的生成器那样工作。
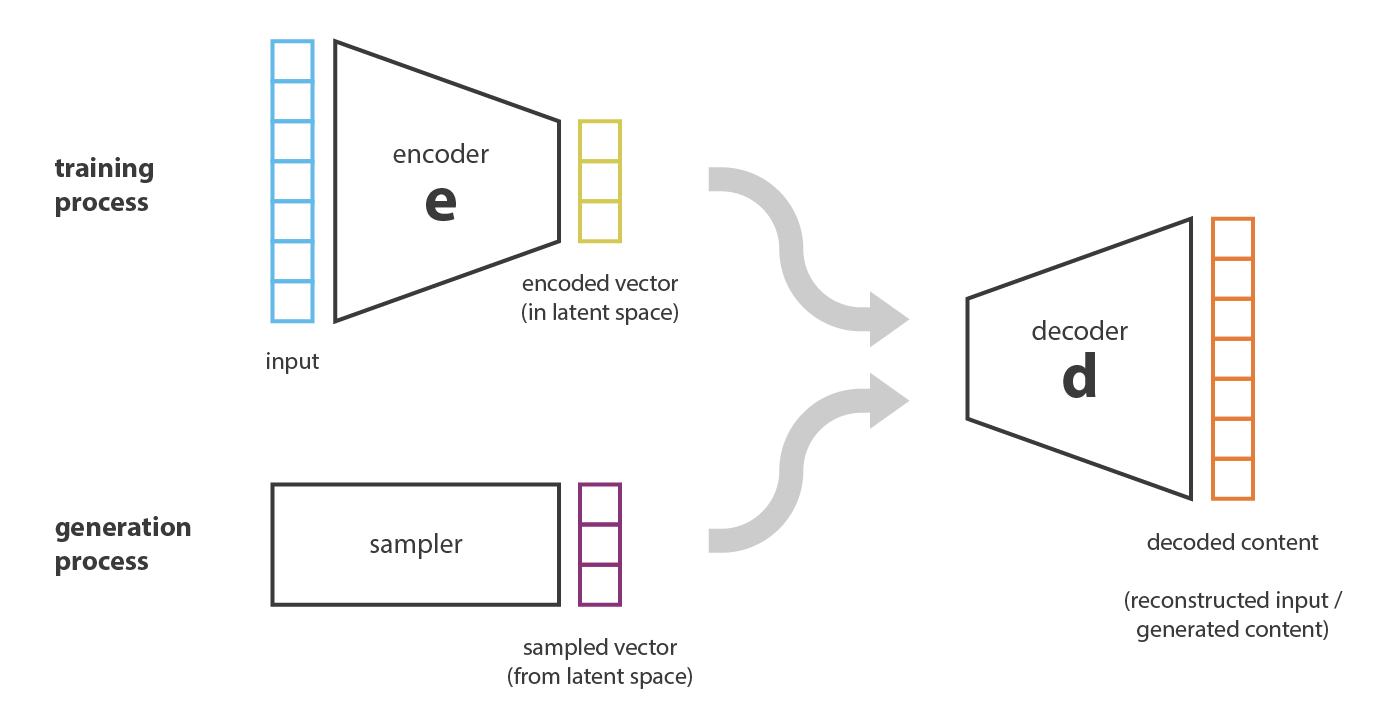
但是,正如我们在上一节中讨论的那样,autoencoders 的隐空间的正则性是一个难点,这取决于初始空间中数据的分布,隐空间的大小和 encoder 的架构。因此,很难先验地确保 encoder 会以与我们刚刚描述的生成过程兼容的方式组织隐空间。
为了说明这一点,让我们考虑之前给出的示例,在该示例中,我们描述了一种强大的 autoencoders,强大到可以将任何 N 个初始训练数据映射到实数轴上(每个数据点都被编码为实数值),并且可以没有任何重建损失地 decode。在这种情况下,autoencoders 的高自由度使得可以在没有信息损失的情况下进行 encode 和 decode(尽管隐空间的维数较低),这样会导致严重的过拟合,意味着一旦 decode,隐空间的某些点将给出无意义的内容。如果我们极端地任意选择此一维空间中的样本,我们可以注意到 autoencoders 隐空间正则性问题要比这更为普遍。
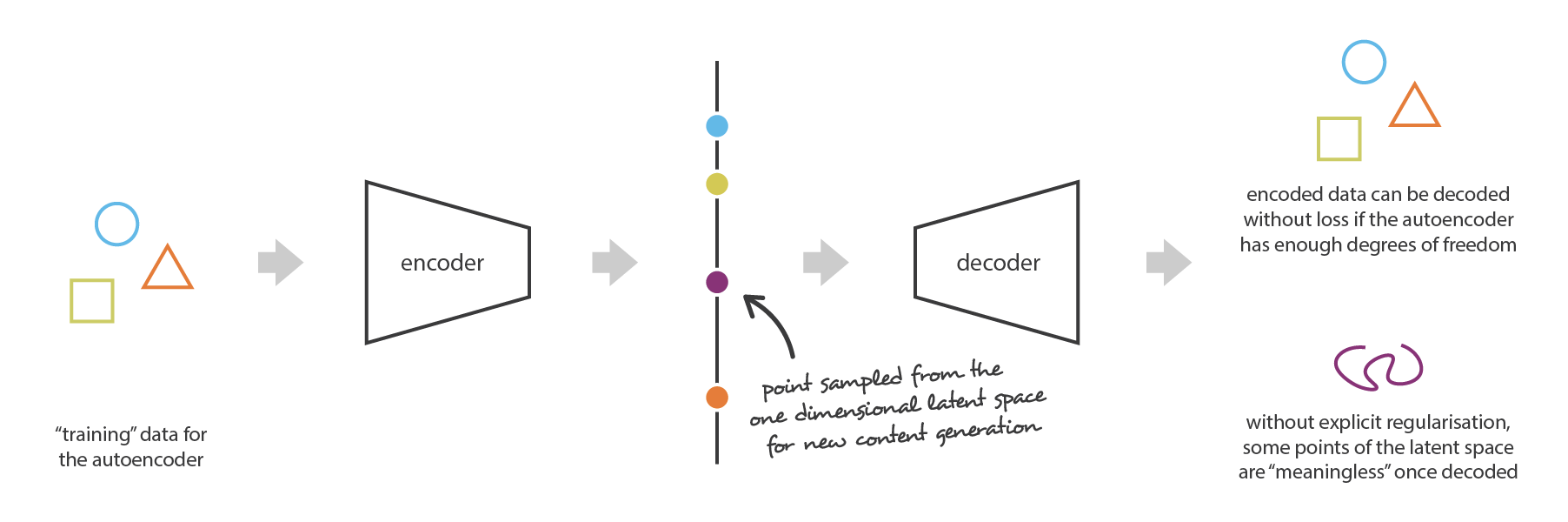
其实这种现象是很正常的。 在 autoencoders 的任务中,autoencoders 仅仅尽可能减少重建损失而不在乎如何组织隐空间。 因此,如果我们对架构定义不好,那么在训练期间,神经网络会利用过拟合来尽其所能来完成其任务,除非我们对其进行正则化。
variational autoencoders 的定义
为了能够将我们的 autoencoders 的 decoder 用于生成数据,我们必须确保隐空间足够正则化。一种解决方案是在训练过程中显式地正则化。 因此,可以将 variational autoencoders 定义为一种 autoencoder,这种 autoencoder 能对其进行正则化训练以避免过拟合并确保隐空间具有能够生成数据的良好属性。
就像标准 autoencoders 一样,variational autoencoders 是一种既由 encoder 又由 decoder 组成的架构,经过训练以使 encoded-decoded 后的数据与初始数据之间的重构误差最小。 但是,为了对隐空间正则化,我们对 encode-decode 过程进行了一些修改:我们将输入 encode 为一个隐空间上的分布,而不是将输入 encode 为单个点。 然后对模型进行如下训练:
- 首先,将输入 encode 为在隐空间上的分布
- 第二,从该分布中采样隐空间中的一个点
- 第三,对采样点进行 decode 并计算出重建误差
- 最后,重建误差通过网络反向传播
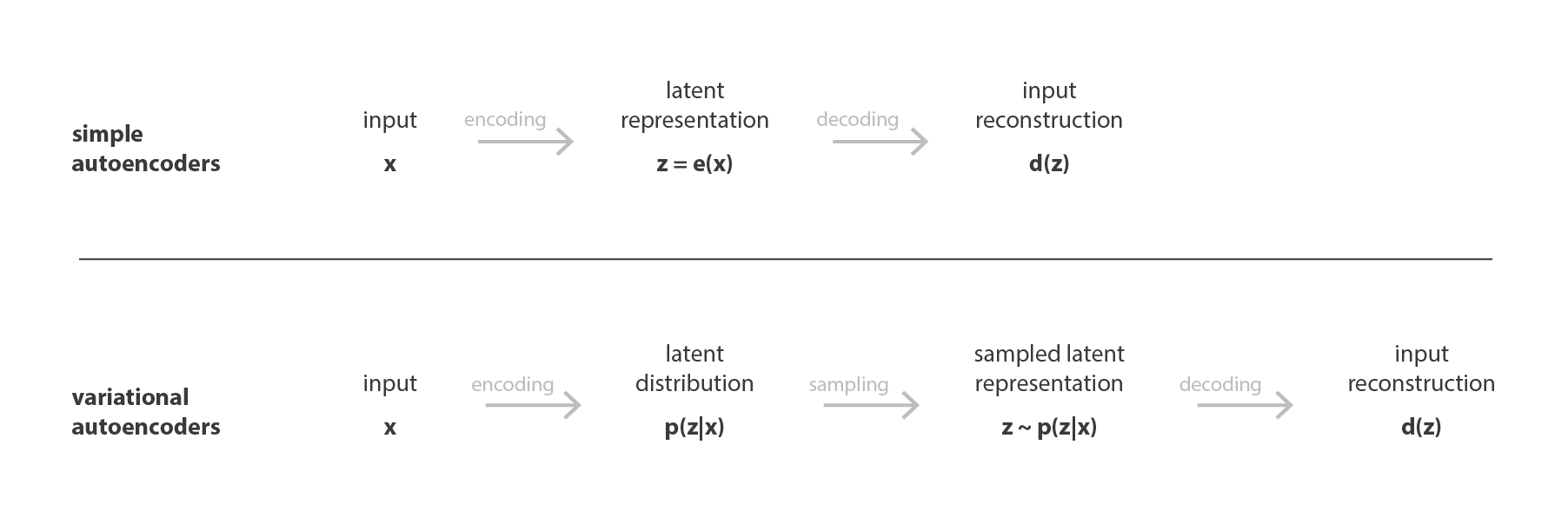
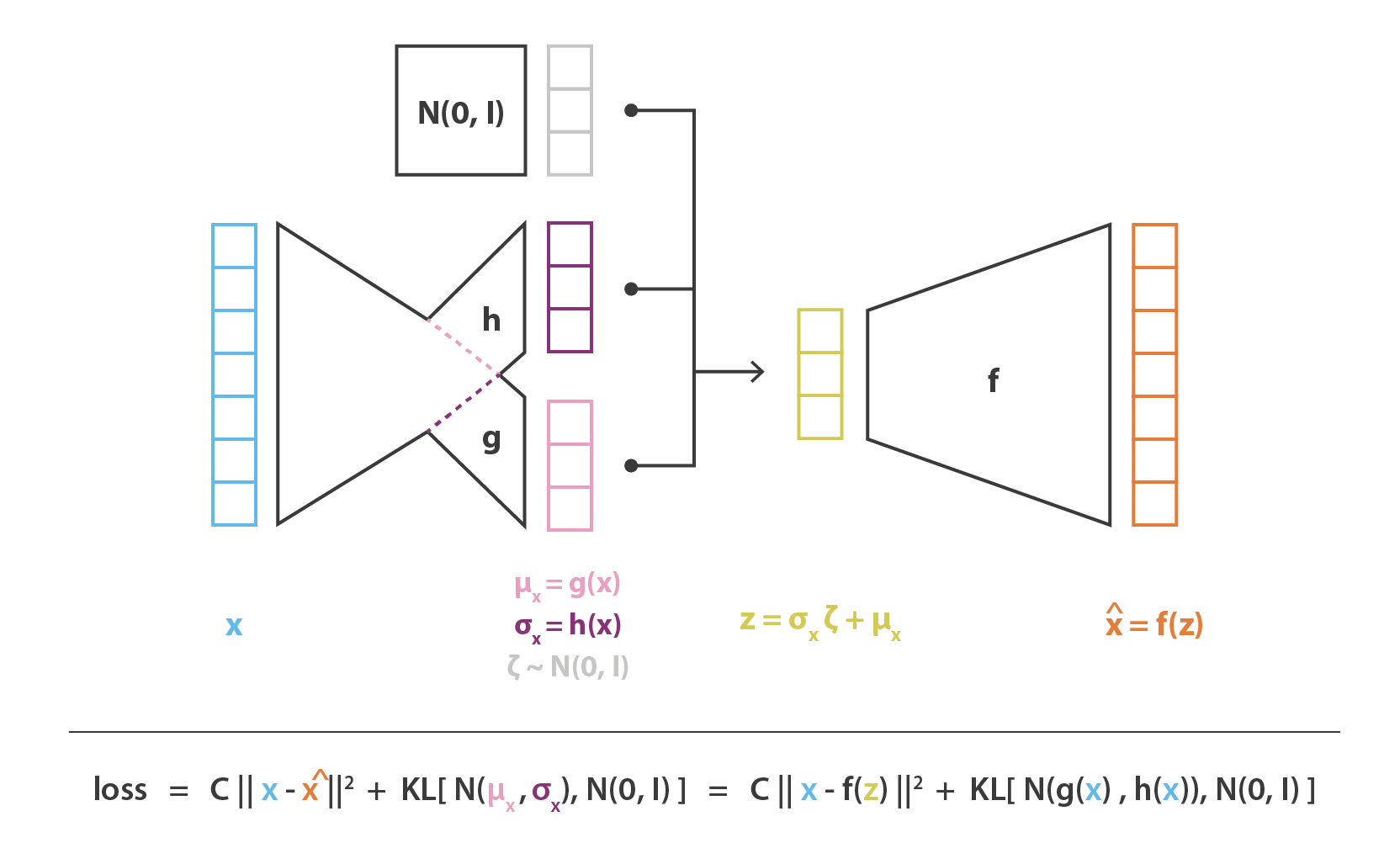
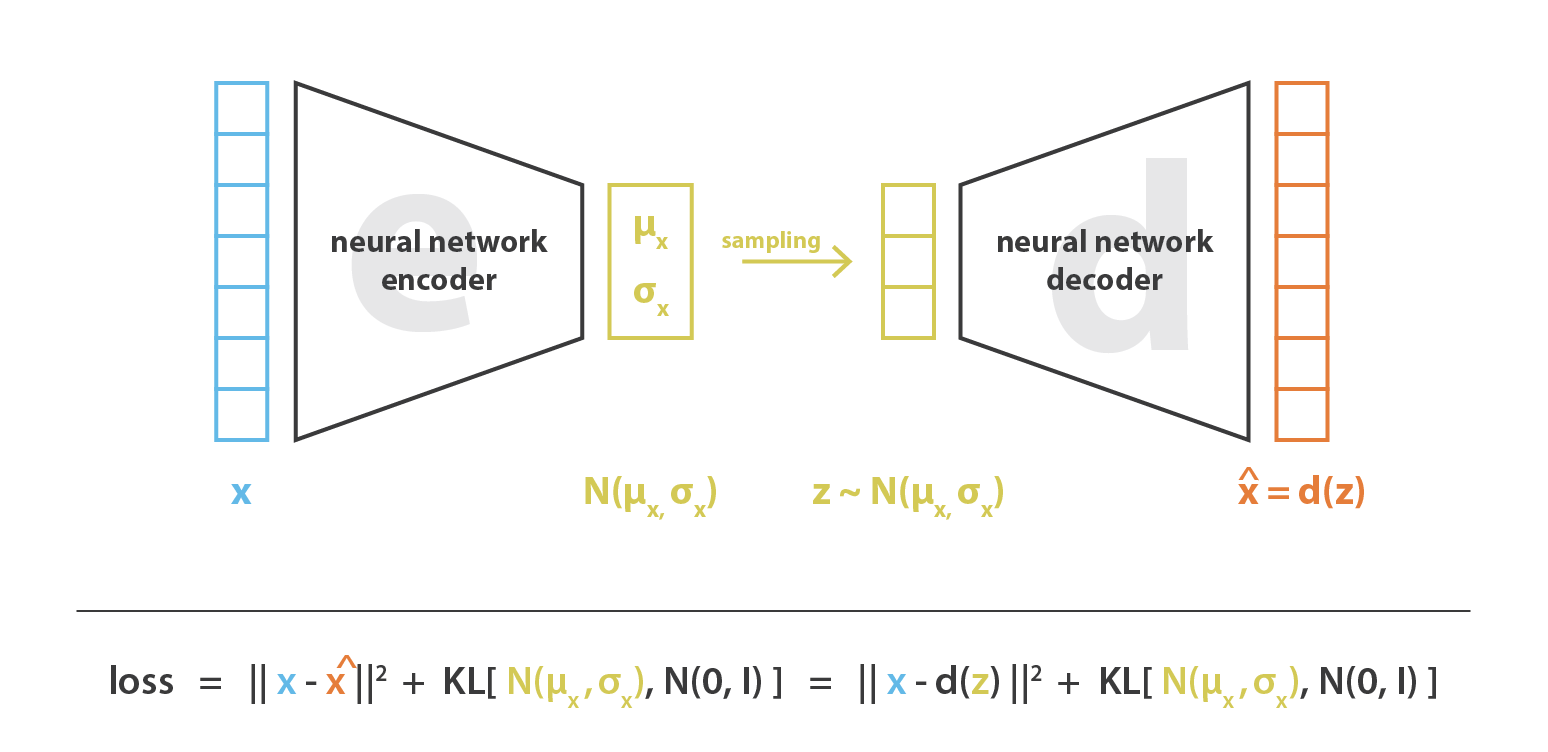
在实际应用中,我们会选择正态分布作为 encoder 的分布,以便可以训练 encoder 返回描述这些高斯分布的均值和协方差矩阵。将输入的数据 encode 为具有一定方差而不是单个点的分布的原因是,它可以非常自然地表达隐空间正则化:encoder 返回的分布需要强制接近标准正态分布。下一小节中,我们将通过这种方式确保隐空间的局部和全局正则化(局部由方差控制,全局由均值控制)。
因此,在训练 VAE 时最小化的损失函数由“重构项”(在最后一层上)和“正则化项”(在隐藏层上)组成,“重构项”倾向于使 encoding-decoding 方案表现得尽可能好,“正则化项”通过使 encoder 返回的分布接近标准正态分布来正则化隐空间。该正则化项表示为返回的分布与标准高斯之间的 Kulback-Leibler 散度。我们可以注意到,两个高斯分布之间的 KL 散度具有封闭形式,可以直接用两种分布的均值和协方差矩阵来表示。
正则化的直观理解
我们直接用两张图来代替原文的大段描述:

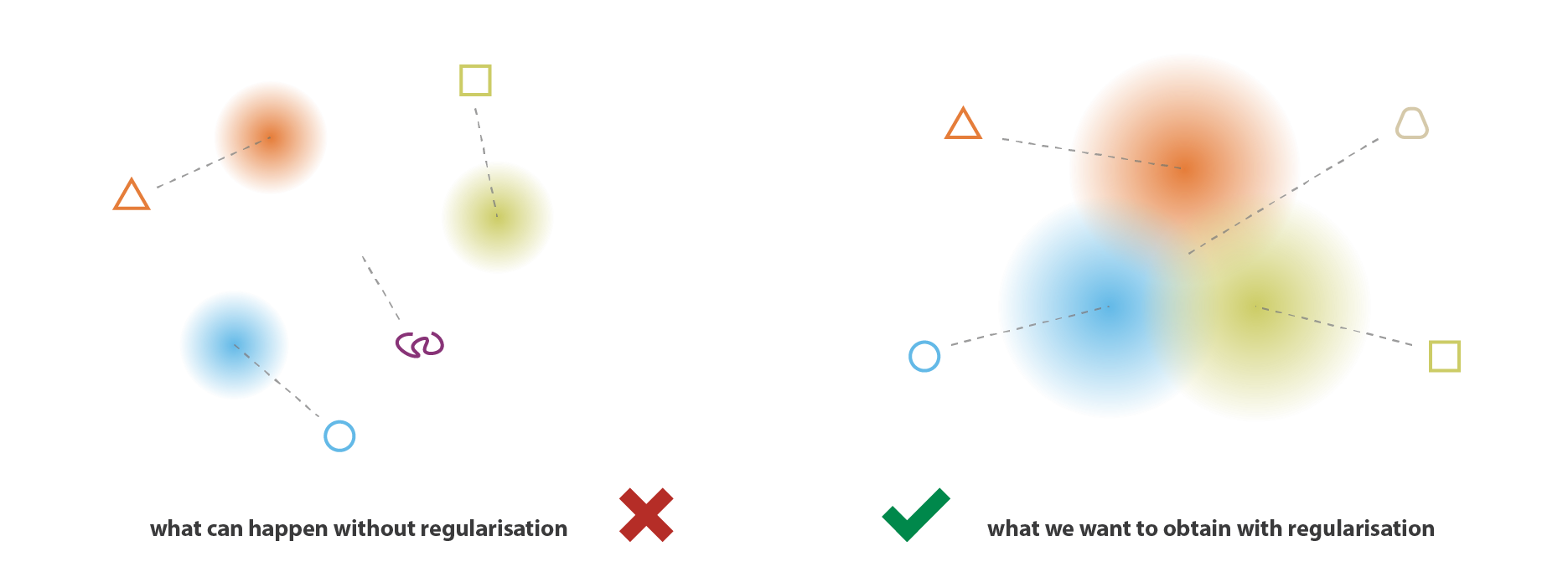
VAEs 中的数学
在上一小节中,我们给出了以下直观的理解:VAE 就是将输入 encode 为分布而不是点的 autoencoder,并且通过将 encoder 返回的分布约束为接近标准正态分布而得到正则化的隐空间。 在本小节中,我们将对 VAE 进行更数学化的介绍,这将使我们能够更严格地证明正则化项的合理性。 为此,我们将建立一个概率框架并使用变分推断。
概率框架及一些假设
首先,定义一个概率图模型来描述我们的数据。 我们用 \(x\) 表示我们原始数据的变量,并假定 \(x\) 是由未直接观测到的隐变量 \(z\)(encoded 后的表征)生成的。 因此,对于每个数据点,假定以下两个步骤的生成过程:
- 首先,隐变量 \(z\) 是由一个先验 \(p(z)\) 采样而来的
- 其次,数据 \(x\) 是由条件似然分布 \(p(x|z)\) 采样而来的
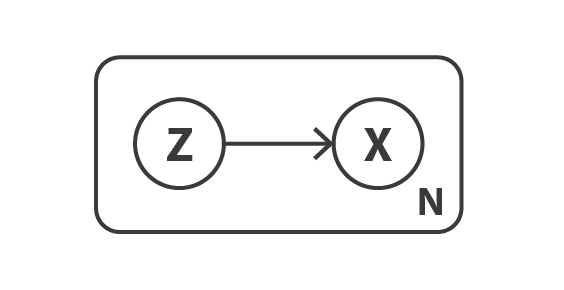
根据这种概率模型,我们可以重新定义 encoder 和 decoder 的概念。 与只考虑确定性 encoder 和 decoder 的简单 autoencoder 相反,我们现在将考虑这两个对象的概率版本。 “概率decoder”由 \(p(x|z)\)定义,用来描述给定 encoded 变量的 decoded 变量的分布,而 “概率encoded”由 \(p(z|x)\) 定义,用来描述给定 decoded 变量的 encoded 变量的分布。
至此,我们已经可以注意到,在简单的 autoencoder 中所缺少的隐空间正则化出现在数据生成过程的定义中:隐空间中的 encoded 表征 \(z\) 实际上被假定遵循先验分布 \(p(z)\)。 另外,我们还可以回想一下著名的贝叶斯定理,先验 \(p(z)\),似然 \(p(x|z)\) 和后验 \(p(z|x)\) 之间的联系。 \[ p(z | x)=\frac{p(x | z) p(z)}{p(x)}=\frac{p(x | z) p(z)}{\int p(x | u) p(u) d u} \] 现在假设 \(p(z)\) 是标准高斯分布,\(p(x|z)\) 也是一个高斯分布,且它的均值由一个确定性函数 \(f(z)\) 定义,协方差矩阵是某一个常量 \(c\) 乘以单位矩阵 \(I\) 而来。函数 \(f\) 暂且是一堆函数 \(F\) 中的一个,我们稍后再去选择这个函数。现在我们有 \[ \begin{array}{l}{p(z)=\mathcal{N}(0, I)} \\ {p(x | z) \equiv \mathcal{N}(f(z), c I) \quad f \in F \quad c>0}\end{array} \] 现在,假设 \(f\) 已经是最优了且固定了下来,那么理论上因为我们知道了 \(p(z)\) 和 \(p(x|z)\) ,就可以使用贝叶斯理论来计算 \(p(z|x)\) ,也就是经典的贝叶斯推理问题。但是,这种贝叶斯计算一般是很困难,无法完成的(因为分母的积分没有办法计算),所以需要一种近似的方法比如变分推断 variational inference。
变分推断公式
在统计学中,变分推断(VI)就是用来近似复杂分布的一种方法。这个想法就是要使用一个参数化的分布族(例如高斯族,其参数是均值和协方差),在该族中寻找目标分布的最佳近似值。 该族中最好的元素是使给定的近似误差(在大多数情况下,近似与目标之间的 KL 散度)最小的一种元素,并通过梯度下降来求得该参数。
现在我们用一个高斯分布 \(q_x(z)\) 来近似 \(p(z|x)\) 。它的均值与方差由函数 \(g\) 和 \(h\) 定义,这两个函数均是 \(x\) 的函数。同时这两个函数分别属于函数族 \(G\) 和 \(H\)。 \[ q_{x}(z) \equiv \mathcal{N}(g(x), h(x)) \quad g \in G \quad h \in H \] 那么现在我们已经定义了一族要进行变分推断的近似函数,并且要在这些函数中通过优化 \(f\) 和 \(h\) 来找到最优的近似函数(其实就是优化 \(f\) 和 \(h\) 的参数),这个优化就是要最小化近似分布与目标分布 \(p(z|x)\) 之间的 KL 散度。换句话说,我们要找到最优的 \(g^*\) 与 \(f^*\) 以满足: \[ \begin{aligned}\left(g^{*}, h^{*}\right) &=\underset{(g, h) \in G \times H}{\arg \min } K L\left(q_{x}(z), p(z | x)\right) \\ &=\underset{(g, h) \in G \times H}{\arg \min }\left(\mathbb{E}_{z \sim q_{x}}\left(\log q_{x}(z)\right)-\mathbb{E}_{z \sim q_{x}}\left(\log \frac{p(x | z) p(z)}{p(x)}\right)\right) \\ &=\underset{(g, h) \in G \times H}{\arg \min }\left(\mathbb{E}_{z \sim q_{x}}\left(\log q_{x}(z)\right)-\mathbb{E}_{z \sim q_{x}}(\log p(z))-\mathbb{E}_{z \sim q_{x}}(\log p(x | z))+\mathbb{E}_{z \sim q_{x}}(\log p(x))\right) \\ &=\underset{(g, h) \in G \times H}{\arg \max }\left(\mathbb{E}_{z \sim q_{x}}(\log p(x | z))-K L\left(q_{x}(z), p(z)\right)\right) \\ &=\underset{(g, h) \in G \times H}{\arg \max }\left(\mathbb{E}_{z \sim q_{x}}\left(-\frac{\|x-f(z)\|^{2}}{2 c}\right)-K L\left(q_{x}(z), p(z)\right)\right) \end{aligned} \] 在倒数第二个式子中,即在估计后验 \(p(z|x)\) 的过程中,我们可以看到一种权衡:既要最大化初始观测数据的似然(第一项,最大化期望 log-likelihood),又要更靠近先验分布(第二项,最小化 \(q_x(z)\) 与 \(p(z)\) 之间的 KL 散度)。这种权衡在贝叶斯推断问题中很自然,并且表达了我们想要找到在初始数据的置信度与先验的置信度之间的平衡。
到目前为止,我们假设函数 \(f\) 是已知并且是固定的,并且在这种假设下我们可以使用变分推断的方法来近似后验 \(p(z|x)\) 。但在实际操作中,这个函数 \(f\) ,也就是定义了 decoder 的函数是不可知的,也同样的需要在一堆函数族中进行选择。为此,让我们回想一下我们的最初目标就是要去找到一个性能良好的 encoding-decoding 方案,且该方案的隐空间是正则化的,并足够正则化来生成新数据。如果正则性主要是由先验分布所决定的,那么整个 encoding-decoding 的性能主要取决于函数 \(f\) 的选择。也的确,由于 \(p(z|x)\) 可以由 \(p(z)\) 和 \(p(x|z)\) 近似(用变分推断)而来且 \(p(z)\) 是一个简单的标准高斯分布,因此在我们的模型中需要优化的只有两个:参数 \(c\) ,控制着似然的方差,和函数 \(f\) ,控制着似然的均值。
我们之前也提到过,我们可以从 \(F\) 中选择去任意的 \(f\) 来得到 \(p(z|x)\) 的最佳近似 \(q^*_x(z)\) 。如果不管它的概率属性,我们想要做的就是让 encoding-decoding 性能越高越好,那么我们更想要去选择能最大化在给定 \(z\) 下(\(z\) 从 \(q^*_x(z)\) 采样而来)的 \(x\) 的期望 log-likelihood 的那些 \(f\) 。也就是说,对于一个给定的输入 \(x\) ,当我们从 \(q^*_x(z)\) 采样 \(z\) ,又从 \(p(x|z)\) 采样得到 \(\hat{x}\) 时,我们想要去最大化 \(\hat{x}=x\) 的概率。因此,我们想要找到的 \(f^*\) 满足: \[ \begin{aligned} f^{*} &=\underset{f \in F}{\arg \max } \mathbb{E}_{z \sim q_{x}^{*}}(\log p(x | z)) \\ &=\underset{f \in F}{\arg \max } \mathbb{E}_{z \sim q_{x}^{*}}\left(-\frac{\|x-f(z)\|^{2}}{2 c}\right) \end{aligned} \] 其中函数 \(f\) 决定了 \(q^*_x(z)\)。将上面这些都联系起来,我们其实就是要去找最优 \(f^*,g^*,h^*\),使: \[ \left(f^{*}, g^{*}, h^{*}\right)=\underset{(f, g, h) \in F \times G \times H}{\arg \max }\left(\mathbb{E}_{z \sim q_{x}}\left(-\frac{\|x-f(z)\|^{2}}{2 c}\right)-K L\left(q_{x}(z), p(z)\right)\right) \] 我们可以将这个目标函数与之前介绍的 VAEs 的直观理解联系起来:第一项是 \(x\) 与 \(f(z)\) 之间的重构误差,第二项是 \(q_x(z)\) 与 \(p(z)\) (也就是标准高斯)之间的 KL 散度。我们也可以注意到常量 \(c\) 平衡着这两项:\(c\) 越大,模型中的概率 decoder \(f(z)\) 周围的方差就越大,也因此我们更倾向正则化项。若 \(c\) 小,则相反。
引入神经网络
至此,我们建立了一个依赖于三个函数 \(f,g,h\) 的概率模型,并用变分推断的方法解释了优化问题来得到最优 \(f^*,g^*,h^*\) 。由于我们没有办法遍历整个函数族,所以我们要限制优化的范围,并用神经网络来表达 \(f,g,h\) 。
在实际中,\(g\) 和 \(h\) 不会被分开形成两个独立的网络,而是共享一部分的权重: \[ g(x)=g_{2}\left(g_{1}(x)\right) \quad h(x)=h_{2}\left(h_{1}(x)\right) \quad g_{1}(x)=h_{1}(x) \] 我们在 \(q_x(z)\) 的协方差矩阵中定义过,\(h(x)\) 应该是一个方阵。但为了简单起见,我们假设 \(p(z|x)\) 的近似 \(q_x(z)\) 是一个对角协方差矩阵的多维正态分布。在这个假设下 \(h(x)\) 就是一个简单的向量,代表协方差矩阵的对角线,并且长度与 \(g(x)\) 相同,当然这会降低近似 \(p(z|x)\) 的准确性。
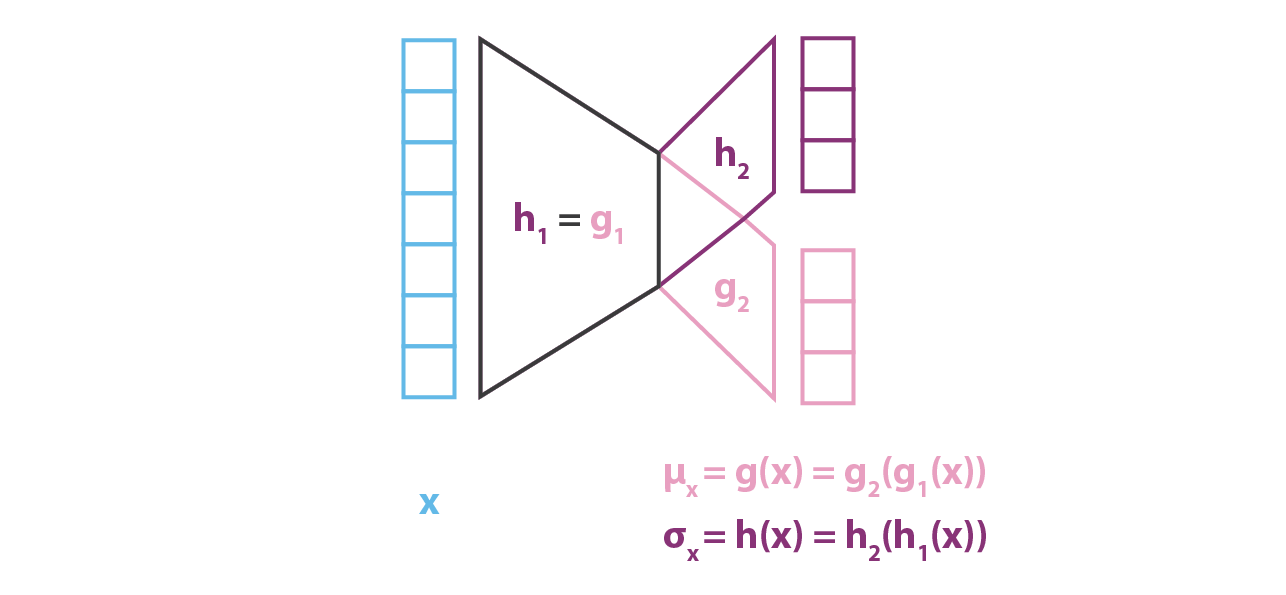
与 encoder 部分相反,我们假设 \(p(x|z)\) 是一个有着固定方差的高斯分布。函数关于 \(z\) 的函数 \(f\) 定义了这个高斯分布的均值,同时也用一个神经网络来表示:
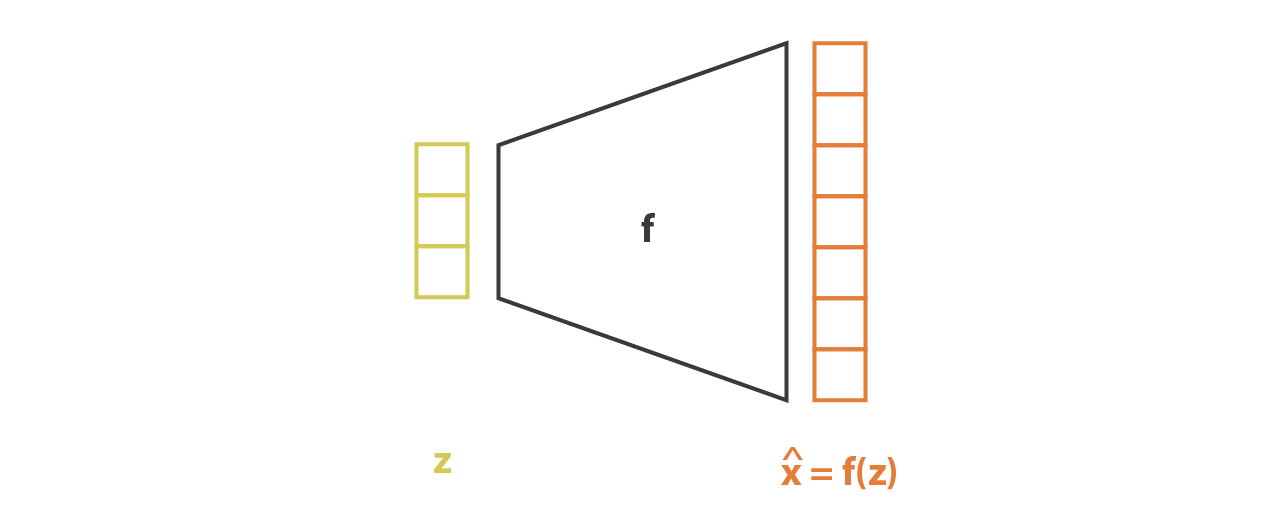
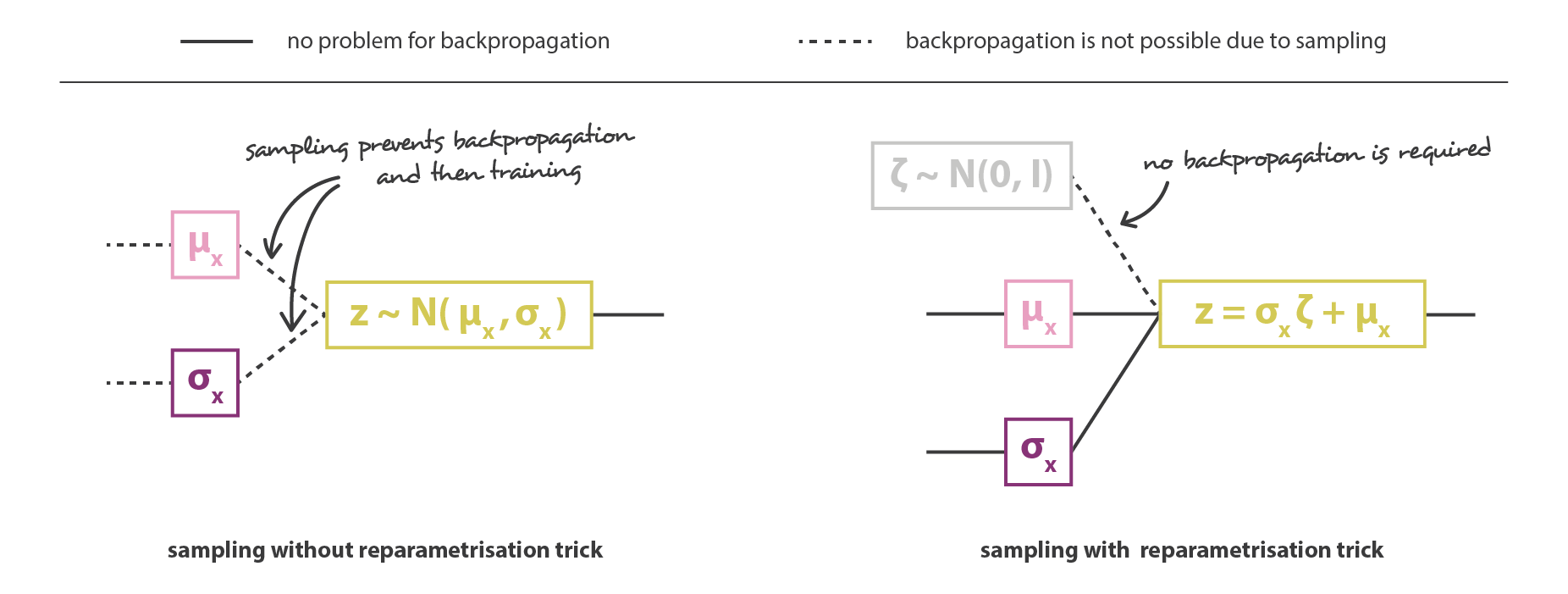
然后把 encoder 和 decoder 两部分串联起来就可以组成 VAE 的整体架构了。但在训练过程中,我们必须注意从 encoder 返回的分布中采样的方式,因为采样的过程必须允许误差通过网络反向传播。尽管是在整个架构的一半进行随机采样,但有一个重参数技巧让梯度下降成为可能。因为 \(z\) 是遵循均值为 \(g(x)\) 方差为 \(h(x)\) 的高斯分布,它也可以被表示为: \[
z=h(x) \zeta+g(x) \quad \zeta \sim \mathcal{N}(0, I)
\] 
最终,VAE 架构的目标函数可以由前面小节给出,其中,理论上期望可以用蒙特卡洛来估计。我们定义 \(C=1/(2c)\) ,那么损失函数即为一个重构项,一个正则化项还有一个常数来定义这两项的权重。