DeepMind ICLR 2018 的论文 Noisy Networks for Exploration 介绍一种将参数化的噪音加入到神经网络权重上去的方法来增加强化学习中的探索,称为 NoisyNet 。噪音的参数可以通过梯度来进行学习,非常容易就能实现,而且只增加了一点计算量,在 A3C ,DQN 算法上效果不错。
NoisyNet 的思想很简单,就是在神经网络的权重上增加一些噪音来起到探索的目的。
我们将噪音参数定义为: \(\theta \stackrel{\rm def}{=} \mu +\Sigma\odot\varepsilon\) ,其中 \(\zeta\stackrel{\rm def}{=}(\mu,\Sigma)\) 为可被学习的参数向量,\(\varepsilon\) 是均值为 0 的固定的噪音向量,\(\odot\) 表示向量各元素相乘。原本神经网络的损失函数现在要包裹一层 \(\varepsilon\) 的期望:\(\bar L(\zeta) \stackrel{\rm def}{=} \mathbb{E}\left[L(\theta)\right]\) ,所以现在优化的是参数 \(\zeta\) 。
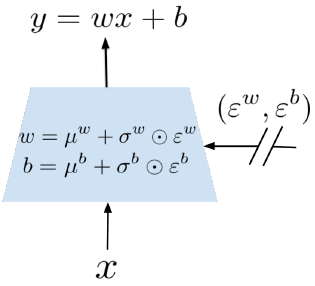
举个例子,如果一个神经网络的有 \(p\) 个输入,\(q\) 个输出,表示为: \[ y=wx+b \] 其中 \(x\in \mathbb{R}^{p}\) 是神经网络的输入, \(w\in\mathbb{R}^{q\times p}\) 为权重矩阵,\(b\in\mathbb{R}^q\) 是偏差向量。经过 NoisyNet 修改过后的神经网络为: \[ y \stackrel{\rm def}{=} (\mu^w+\sigma^w\odot\varepsilon^w) x+ \mu^b +\sigma^b\odot\varepsilon^b \] 也就是说 \(\mu^w+\sigma^w\odot\varepsilon^w\) 代替了 \(w\) ,\(\mu^b +\sigma^b\odot\varepsilon^b\) 代替了 \(b\) ,下图展示了这个过程:
对于 \(\varepsilon\) 的生成有两种方式:
- 独立高斯噪音:噪音矩阵中每个元素的生成都是独立的,也就是说 \(\varepsilon^w\) 中的每个 \(\varepsilon^w_{i,j}\) 都独立地来自于高斯分布。这样子神经网络的每层就需要 \(pq+q\) 个噪音变量
- 分解高斯噪音:我们用两个初始向量 \(\varepsilon_i\) 和 \(\varepsilon_j\) ,长度分别为 \(p\) 和 \(q\) 来表示 \(\varepsilon^w_{i,j}\) 和 \(\varepsilon^b_j\)
\[ \begin{align*} \varepsilon^w_{i,j}& = f(\varepsilon_i)f(\varepsilon_j), \\ \varepsilon^b_j& = f(\varepsilon_j) \end{align*} \]
其中 \(f\) 为实值函数,作者使用了 \(f(x) = \mathrm{sgn}(x)\sqrt{|x|}\) 。那么这个时候损失函数的梯度可以写为: \[ \nabla \bar L(\zeta)= \nabla \mathbb{E}\left[L(\theta)\right]= \mathbb{E}\left[\nabla_{\mu,\Sigma} L(\mu + \Sigma\odot \varepsilon) \right] \] 作者将 NoisyNet 运用到了 DQN, Dueling DQN, A3C 上,具体算法可以参考论文附录
参考
Fortunato, Meire, Mohammad Gheshlaghi Azar, Bilal Piot, Jacob Menick, Ian Osband, Alex Graves, Vlad Mnih, et al. 2017. “Noisy Networks for Exploration.” ArXiv:1706.10295 [Cs, Stat], June. http://arxiv.org/abs/1706.10295.

