论文 Incentivizing Exploration In Reinforcement Learning With Deep Predictive Models 提出了一种基于模型的,为 Reward Function 增加 Bonus 的方法来刺激 agent 进行探索。
Introduction
Exploration versus exploitation tradeoff 一直是强化学习中的一个大问题。之前有虚度哦效果很好的方法比如基于贝叶斯的 Bayesian Exploration Bonuses (BEB) ,但它们往往依赖于访问每一个 state-action pair 的次数,所以很难运用到大规模强化学习任务中。另外,尽管 Boltzman exploration 和 Thompson sampling 能很好地提高 ε-greedy 探索策略,但作者发现基于模型的奖励探索机制效果更好。
Model Learning For Exploration Bonus
\[ \mathcal{R}_{\text{Bonus}}(s,a)=\mathcal{R}(s,a)+\beta\mathcal{N}(s,a) \]
该公式为本论文最核心的奖励函数公式,它在原有 reward function 基础上加入了一个 novelty function \(\mathcal{N}(s,a): \mathcal{S}\times\mathcal{A}\rightarrow[0,1]\) 来表示 state-action pair 的新颖程度,如果该配对值得探索,则 novelty function 值就会增大,反之减小。
用 \(\sigma(s)\) 来重新编码状态 \(s\) ,用 \(\mathcal{M}_\phi: \sigma(\mathcal{S})\times\mathcal{A}\rightarrow\sigma(\mathcal{S})\) 来表示环境模型,即根据 \(t\) 时刻的状态 \(s\) 与行为 \(a\) 来预测 \(t+1\) 时刻的状态。
对于一个 transition \((s_t,a_t,s_{t+1})\) 我们可以定义模型的误差: \[ e(s_t,a_t)=||\sigma(s_{t+1})-\mathcal{M}_\phi(\sigma(s_t),a_t)||_2^2 \] 令 \(\overline{e_T}\) 表示 \(T\) 时刻归一化的模型误差:\(\overline{e_T}=\frac{e_T}{\max_{t\le T}\{e_t\}}\) ,则我们的 novelty function 可以写成: \[ \mathcal{N}(s_t,a_t)=\frac{\overline{e_t}(s_t,a_t)}{t*C} \] 其中 \(C>0\) 为衰减常数。修改过的奖励函数为: \[ \mathcal{R}_{\text{Bonus}}(s,a)=\mathcal{R}(s,a)+\beta\left(\frac{\overline{e_t}(s_t,a_t)}{t*C}\right) \] 当我们在对 state-action pair 建模的能力加强时,我们对该状态了解的更多,因此该状态的 novelty 降低。当我们对 state-action pair 理解不够时,我们则要增加它的 novelty 。
Deep Learning Architectures
Autoencoders
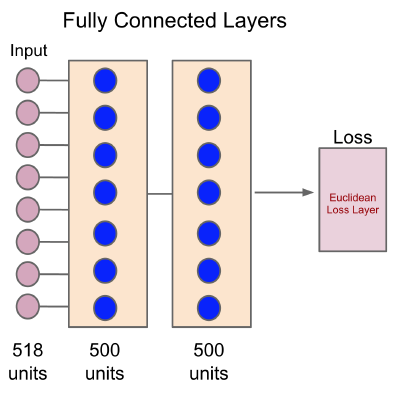
作者经过实验,模型对于原始状态的预测效果不好,为了解决这个问题,作者根据论文 Reducing the dimensionality of data with neural networks 引入了 \(\sigma\) 函数来对原始状态进行重新编码,获得一个低维度的状态表示量。神经网络架构为:
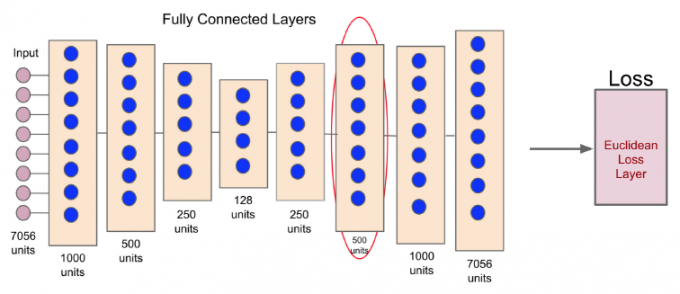
输入为原始状态,隐藏层的最后一层大小与原始状态大小相同,输出为一个欧氏距离误差层,尽可能减少最后的状态特征与原始输入的差异。红色圈圈出来的即为降低了维度的 \(\sigma(s)\) 。
Model Learning Architecture
模型网络的构建很简单,输入为重新编码过的状态与行为对 \((\sigma(s),a)\) 输出为下一时刻预测的编码状态。