Learning to Communicate to Solve Riddles with Deep Distributed Recurrent Q-Networks

在 Learning to Communicate to Solve Riddles with Deep Distributed Recurrent Q-Networks 论文中，作者提出了一种 deep distributed recurrent Q-networks (DDRQN) 方法，它可以解决多个智能体互相之间的交流协作问题，使智能体之间从无到有达成一种交流协议。论文主要针对两个著名的谜题：囚犯帽子谜题 (Hats Riddle) 与 囚犯开关谜题 (Switch Riddle) 来设计解决方案。

DDRQN

DDRQN 在 DQN 、Independent DQN 和 DRQN 的基础上做了一些改进，主要体现在三个方面：

1. last-action inputs: 每个时刻都给每个智能体提供行为与观察到的状态 (action-observation histories) 作为输入，而不仅仅是观察到的状态 (observation histories) 。因为智能体由于需要进行探索，所以采取的策略是随机的，而加入行为作为输入可以让 RNN 更好地工作。
2. inter-agent weight sharing: 先前的 Independent DQN 也可以用来处理多智能体问题，但每个智能体有其独有的 \(Q\) 参数，并且是同时独立地进行学习，但 Independent DQN 会产生收敛性问题，所以 DDRQN 采用了多个智能体共享一套 \(Q\) 函数进行学习。尽管如此，每个智能体当然也会采取不同的行为方式因为它们观察到的状态不同，也因此会产生不同的隐藏状态，另外，每个智能体还会额外地接受它们的序号 \(m\) 作为输入。
3. 取消 DQN 中的经验回放特性，因为当多个智能体进行独立的学习时，环境对于每个智能体来说会变的非静态 (non-stationary) ，而经验回访可能会产生一些误导作用。

根据以上的改进，DDRQN 的 \(Q\) 函数形式为 \(Q(o_t^m,h_{t-1}^m,m,a_{t-1}^m,a_t^m;\theta_i)\) ，\(m\) 为智能体的序号，\(o_t^m\) 为部分观察到的状态，\(h_{t-1}^m\) 为 RNN 输出的隐藏状态，\(a_{t-1}^m\) 为之前采取的行为，注意到这里的 \(\theta_i\) 与 \(m\) 无关，以此来实现参数共享。具体算法为：

Multi-Agent Riddles

Hat Riddle

行刑者下令 100 个囚犯排成一列，并且把一顶红色或蓝色的帽子戴到每个囚犯头上。每个囚犯都能看见自己前面所有囚犯戴的帽子，但看不见自己的帽子或自己后面的囚犯所戴的帽子。行刑者从最后那个囚犯开始提问：你戴的帽子是什么颜色？只有答对了，囚犯才能活下来。如果答错，囚犯就会被“安静地处死”。也就是说，其他囚犯能听见这个囚犯说的话，但不可能知道他的回答是否正确。在这场处决的前晚，囚犯们被给予机会讨论一种策略来帮助自己存活。那么，究竟有没有这样一种策略？如果有，它是怎样一种策略？(Poundstone, 2012)

最优策略是所有的囚犯应该达成一种交流的协议：第一个被提问的囚犯也就是最后的那个囚犯能看到除了自己之外的其他所有囚犯的帽子颜色，如果他看到蓝色帽子是奇数个，那么他就回答“蓝色”，否则就回答”红色“，这样一来，其余的囚犯就可以通过观察在他们之前的囚犯的帽子颜色与听在他们之后的囚犯的回答来断定自己帽子的颜色。因此，除了第一个囚犯有 50% 几率被处死以外，其他囚犯都会回答正确而活下来。

我们将这个谜题转换为多智能体强化学习的任务形式：状态空间 \(\textbf{s}=(s^1,\cdots,s^n,a^1,\cdots,a^n)\) ，\(n\) 为总智能体数量，\(s^m\in\{\text{blue},\text{red}\}\) 为第 \(m\) 个智能体的帽子颜色，\(a^m\in\{\text{blue},\text{red}\}\) 为这个智能体在第 \(m\) 步所采取的行动，在其他时刻，第 \(m\) 个智能体所能采取 null 行为。在第 \(m\) 步，第 \(m\) 个智能体所能观察到的状态为 \(o^m=(a^1,\cdots,a^{m-1},s^{m+1},\cdots,s^n)\) 。在回合结束之前，得到的奖励都为 0 ，最后一步所得到的总奖励为 \(r_n=\sum_m\mathbb{I}(a^m=s^m)\)

Switch Riddle

有 100 个新囚犯刚被送入监狱，守卫告诉他们从明天开始每个人都会被安排到独立的牢房中，无法与其他人进行交流。每一天守卫会等概率地随机地有放回地挑选一个囚犯，安排到一个审讯室中，该审讯室中只有一个带有开关的电灯泡。囚犯可以观察这个灯泡的开关情况，也可以切换灯泡的开关，他也可以选择声称他相信所有的囚犯已经都来过这个审讯室了，如果他的声明是正确的，那么所有囚犯都会被释放，但如果这个声明是错的，所有囚犯都会被处死。现在所有囚犯被允许聚到一起讨论，他们能否达成一致策略是的都能被释放？(Wu, 2002)

有许多策略可以解决这个问题，其中一个比较著名的解决方案是：任命一个囚犯为计数员，只有他可以将关闭灯泡的开关，其余的囚犯只能打开开关，并且只能打开一次。因此，如果计数员已经将开关关闭 \(n-1\) 次，这时他就可以选择声称所有囚犯都已经来到过这个审讯室。

我们定义行为空间 \(\textbf{s}=(SW_t,IR_t,s^1,\cdots,s^n)\) ，其中 \(SW_t\in\{\text{on},\text{off}\}\) 代表开关的状态， \(IR_t\in\{1\cdots n\}\) 代表当前是第几个囚犯在审讯室中，\(s^1,\cdots,s^n\in\{0,1\}\) 表示囚犯是否已经进入过审讯室。在 \(t\) 时刻，智能体 \(m\) 可以观察到状态 \(o_t^m=(ir_t,sw_t)\) 其中 \(ir_t=\mathbb{I}(IR_t=m)\) ，如果该囚犯在审讯室中，则 \(sw_t=SW_t\) ，否则为 null 。如果第 \(m\) 个囚犯在审讯室中那么他可以选择行为 \(a_t^m\in\{\text{On},\text{Off},\text{Tell},\text{None}\}\) ，否则只能选择 \(\text{None}\) 。当有囚犯选择 \(\text{Tell}\) 时，回合结束。在回合结束之前，奖励都为 0 ，结束之后，如果所有囚犯都进入过审讯室则奖励为 1 ，否则为 -1 。

Hats Riddle Experiment

本文就简单介绍一下论文中给出的解决 Hats Riddle 所采用的网络结构。

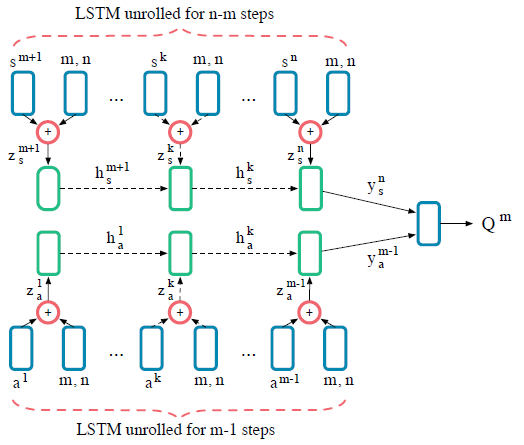
为了要选择行为 \(a^m\) ，整个网络的输入为 \(o^m=(a^1,\cdots,a^{m-1},s^{m+1},\cdots,s^n)\) 还有 \(m\) 与 \(n\) 。它们需要经过两个单层的多层感知机 (MLP) 。\(z_a^k=\text{MLP}[1\times 64](a^k) \oplus \text{MLP}[2\times64](m,n)\) ，\(a^k\) 与 \((m,n)\) 分别经过单层 MLP 维度展开到 64 再进行相加得到 \(z_a^k\) 。\(z_a^k\) 接着经过 LSTM 循环神经网络得到 \(y_a^k\) ，中间的隐藏状态为 \(h_a^k=\text{LSTM}_a[64](z_a^k,h_a^{k-1})\) 。同理，除了观察到的行为之外，还有观察到的剩余 \(n-m\) 个帽子的颜色状态 ，最终定义为 \(y_s^k\) ，\(h_s^k=\text{LSTM}_s[64](z_a^k,h_a^{k-1})\) ，最后两个 LSTM 网络的结果值 \(y_a^{m-1}\) ，\(y_s^n\) 用来估计行为的 \(Q\) 值： \(Q^m=\text{MLP}[128\times64,64\times64,64\times1](y_a^{m-1}||y_s^n)\) 。

以上是针对 Hat Riddle 的神经网络架构，还有一些其他的超参数详细可以看论文中的说明。

参考

Foerster, J. N., Assael, Y. M., de Freitas, N., & Whiteson, S. (2016). Learning to communicate to solve riddles with deep distributed recurrent q-networks. arXiv preprint arXiv:1602.02672.