Fisher's Blog

Sein heißt Werden
Leben heißt Lernen

0%

Deep Reinforcement Learning In Parameterized Action Space

发表于 更新于 分类于 阅读次数： Valine：

论文 Deep Reinforcement Learning In Parameterized Action Space 将 Deep Deterministic Policy Gradient 算法扩展了一下，使 DDPG 可以处理连续的参数化的行为空间 (parameterized action space) 。论文以机器人世界杯 (RoboCup) 的 2D 游戏 Half-Field-Offense (HFO) 为例，构造了深度神经网络并进行训练。

HFO 介绍

简单介绍一下 HFO 游戏的状态、行为空间与我们自定义的奖励函数。

状态空间

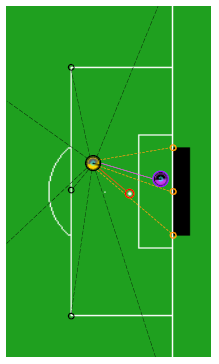
如图所示，我们的 agent 就是这足球上的球员，有着 58 个连续的特征值来表示状态空间，比如该 agent 距球的距离、角球区的距离、禁区角的距离，或者当前的比分，其他球员的信息等等。

行为空间

一个 agent 可以产生四种行为：加速 (Dash) 、转向 (Turn) 、铲球 (Tackle) 和踢球 (Kick) ，每一个行为又有着一道两种连续的参数来控制：

  • Dash (power, direction) ：加速的力度 (power) 在 \([0,100]\) 范围内
  • Turn (direction)
  • Tackle (direction)
  • Kick (power, direction) ：踢球的力度 (power) 在 \([0,100]\) 范围内

所有行为的方向参数在 \([-180,180]\) 角度范围内。

奖励函数

理论上，真正的奖励应该是球员进球，但如果就这么一个奖励信息，对于 agent 来说太稀少了，所以我们手动设计奖励函数。一共有两部分组成：

  • agent 移动到球附近的奖励 (Move To Ball Reward) ：用 \(d(a,b)\) 表示 agent 与 球 (ball) 的距离，\(\mathbb{I}^{kick}\) 表示 agent 是否离球足够近可以踢球，如果是则为 1
  • agent 朝球门踢球后的奖励 (Kick To Goal Reward) ：用 \(d(b,g)\) 表示球与球门的距离，\(\mathbb{I}^{goal}\) 表示踢球之后球是否进门得分，如果是则为 1

有了以上的设计，我们最终的奖励函数为： \[ r_t = d_{t-1}(a,b)-d_t(a,b) + \mathbb{I}_t^{kick} + 3\big(d_{t-1}(b,g)-d_t(b,g)\big) +5\mathbb{I}_t^{goal} \]

参数化行为空间的架构 Parameterized Action Space Architecture

假设我们有一系列的离散的行为 \(A_d=\{a_1,a_2,\cdots,a_k\}\) ，其中每一个行为 \(a\in A_d\) 由 \(m_a\) 个连续参数 \(\{p_1^a,p_2^a,\cdots,p_{m_a}^a\} \in \mathbb{R}^{m_a}\) 的特征向量构成，那么一个行为可以用元组的形式表示： \((a,p_1^a,p_2^a,\cdots,p_{m_a}^a)\) ，因此行为空间可以写为： \(A=\cup_{a\in A_d}(a,p_1^a,p_2^a,\cdots,p_{m_a}^a)\)

在 HFO 游戏中，参数化的行为空间为： \(A=(Dash,p_1^{dash},p_2^{dash})\cup(Turn,p_3^{turn})\cup(Tackle,p_4^{tackle})\cup(Kick,p_5^{kick},p_6^{kick})\)

神经网络架构

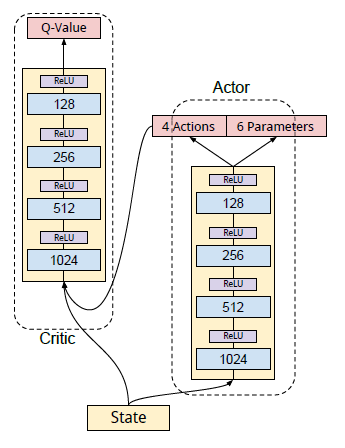
如图，我们用 DDPG 的 actor-critic 形式，其中 actor 与 critic 的隐藏层架构相同。actor 网络的输入为状态向量，输出为行为向量，以前四个为离散的行为 \((Dash,Trun,Tackle,Kick)\) ，后六个为每个行为对应的参数 \((p_1^{dash},p_2^{dash},p_3^{turn},p_4^{tackle},p_5^{kick},p_6^{kick})\) 组成。critic 的输入为状态向量与 actor 所输出的行为向量结合而成的向量，输出则为状态行为价值函数。

按照 DDPG 算法，critic 的损失函数为： \[ L_Q(s,a|\theta^Q) = \bigg( Q(s,a|\theta^Q)-\big( r+\gamma Q(s',\mu(s'|\theta^\mu)'|\theta^Q) \big) \bigg)^2 \] 更新 actor 时用梯度： \[ \nabla_{\theta^\mu} \mu(s) = \nabla_aQ(s,a|\theta^Q) \nabla_{\theta^\mu} \mu(s|\theta^\mu) \]

通过下图也能直观的看出更新 critic 与 actor 所需要的梯度。

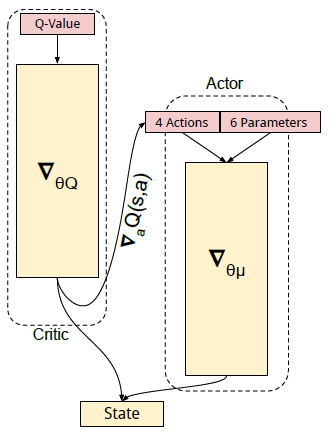
为了使算法更加稳定，同样用了 DDPG 中的两个技巧：设置 target 网络与经验回放机制。

行为的选择与探索 Action Selection and Exploration

对于确定性行为选择来说，每一步 actor 会输出四个离散的行为和六个参数，我们从四个行为中选取值最大的 \(a=\max(Dash,Turn,Tackle,Kick)\) 与对应的参数进行配对，所以 actor 网络会同时选择一个离散的行为去执行，并且用对应的参数来指导如何执行该行为。

连续行为空间与离散空间的探索有点不一样。我们用 ε-greedy 来对参数化的行为空间进行探索：以概率 \(\epsilon\) 随机的选择一个离散的行为 \(a\in A_d\) ，然后再均匀的选取该行为所对应的参数 \(\{p_1^a,p_2^a,\cdots,p_{m_a}^a\}\)

参数空间的上下界 Bounded Parameter Space Learning

再 HFO 游戏中，所有行为的参数总共有两种：一种是表示方向，在 \([-180,180]\) 范围内，另一种表示力度，在 \([0,100]\) 范围内，如果 critic 为 actor 提供梯度并且不加限制地让 actor 持续优化，那么行为参数会非常快的超出各自的上下界。论文中提供了三种方法来控制参数的上下界：

  1. Zeroing Gradients: 这是一种最简单的方法，如果行为参数已经超出上下界，则将 critic 的梯度置零：

\[ \nabla_p = \begin{cases} \nabla_p & \text{if}\ \ p_{\min}<p<p_{\max} \\ 0 &\text{otherwise} \end{cases} \]

  1. Squashing (挤压) Gradients: 使用诸如 \(\tanh\) 函数来为每个参数增加一个激活函数
  2. Inverting Gradients: 该方法综合了前两种方法的思想，如果 critic 的梯度表明需要往正方向更新，则 actor 可以进行持续更新，不过更新幅度会逐渐减小，最终会慢慢收敛到上界，如果此时忽然要往负方向更新，更新幅度则会很快：

\[ \nabla_p=\nabla_p \cdot \begin{cases} (p_\max-p)/(p_\max-p_\min) & \text{if}\ \nabla_p \ \text{suggest increasing} \ p\\ (p-p_\min)/(p_\max-p_\min) &\text{otherwise} \end{cases} \]

参考

Hausknecht, M., & Stone, P. (2015). Deep reinforcement learning in parameterized action space. arXiv preprint arXiv:1511.04143.

Silver D, Lever G, Heess N, et al. Deterministic policy gradient algorithms[C]// International Conference on International Conference on Machine Learning. JMLR.org, 2014:387-395.