Dueling Network Architectures for Deep Reinforcement Learning 论文中， DeepMind 将深度强化学习中的神经网络结构做了一个小的改变，即用 Dueling Network 来表示两个分开的预测量：一个是状态价值函数 (state value function) ，另一个是与状态独立的行为优势函数 (action advantage function)

Dueling Network 架构

对于很多状态来说，不需要去估计该状态下每一个行为的价值，但对于某些状态，选择哪个行为却至关重要，然而同时，对于所有状态来说，状态本身的价值估计都是非常重要的。按照这个直觉思路，我们可以构造出 dueling network ：

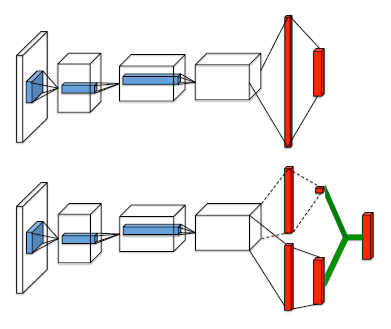
如图所示，上图为传统的神经网络架构，包括前面蓝色的卷积层，与最后红色的全连接层，输出某个状态下对应所有行为的行为价值函数。而下图则是改进过的 dueling network ，前面蓝色卷积层相同，但接着使用了两个分离的全连接层，来分别估计状态价值与优势函数，最后通过绿色线，将两者估计组合起来，输出行为价值函数，也就是说尽管 dueling network 在架构上做了改变，但输出的内容与传统的神经网络架构是相同的。

而正因为输出的是 \(Q\) 值，所以这个架构可以用许多现有的强化学习算法来训练，比如 Double DQN 和 SARSA ，同时它也可以使用之前介绍过的一些增强功能，比如优先经验回放机制等等。

至于怎么把两个全连接层结合成一个行为价值函数需要一些精心的设计。

优势函数用来衡量每个行为的重要性：\(A^\pi(s,a) = Q^\pi(s,a)-V^\pi(s)\) ，由于 \(V^\pi(s) = \mathbb{E}_{a\sim\pi(s)}[Q^\pi(s,a)]\) 则 \(\mathbb{E}_{a\sim\pi(s)}[A^\pi(s,a)] = 0\) 。对于一个确定性策略 \(a^*=\arg\max_{a'\in\mathcal{A}} Q(s,a')\) ，那么 \(Q(s,a^*) = V(s)\) ，因此 \(A(s,a^*)=0\)

对于上图中的 dueling network ，我们可以定义一个全连接层为 \(V(s;\theta,\beta)\) ，另一个全连接层为 \(A(s,a;\theta,\alpha)\) ，其中 \(\theta\) 表示共用卷积层的参数，\(\alpha,\beta\) 表示两个全连接层的参数。那么使用优势函数的定义，我们可以得到： \[ Q(s,a;\theta,\alpha,\beta) = V(s;\theta,\beta) + A(s,a;\theta,\alpha) \] 注意到为了得到 \(Q\) 值，我们需要将 \(V\) 重复使用 \(|\mathcal{A}|\) 次。

然而，\(Q(s,a;\theta,\alpha,\beta)\) 只是真实 \(Q\) 值的一个参数化估计，更进一步，我们也不能认为 \(V(s;\theta,\beta)\) 就是一个好的状态价值函数估计，同理 \(A(s,a;\theta,\alpha)\) 也不一定是优势函数的合理估计。

这个合并的公式是不可辨别的 (unidentifiable) ，因为我们无法通过 \(Q\) 值来恢复出唯一的 \(V\) 和 \(A\) 。比如为 \(V(s;\theta,\beta)\) 加上一个常数，为 \(A(s,a;\theta,\alpha)\) 减去一个常数，都能得到相同的 \(Q\) 值。在实际学习中，如果直接使用上述公式，缺乏可辨别性可能会导致糟糕的学习表现。

为了解决可辨别性问题 (identifiability) ，我们可以强制让选中的行为所对应的优势函数为 0 ，所以可以作如下映射： \[ Q(s,a;\theta,\alpha,\beta) = V(s;\theta,\beta) + (A(s,a;\theta,\alpha) -\max_{a'\in |\mathcal{A}|}A(s,a';\theta,\alpha) ) \] 现在 \(a^*=\arg\max_{a'\in\mathcal{A}}Q(s,a';\theta,\alpha,\beta) = \arg\max_{a'\in\mathcal{A}}A(s,a';\theta,\alpha)\) ，此时可以得到 \(Q(s,a^*;\theta,\alpha,\beta) = V(s;\theta,\beta)\)

还可以用平均值来代替最大值函数： \[ Q(s,a;\theta,\alpha,\beta) = V(s;\theta,\beta) + \left(A(s,a;\theta,\alpha) - \frac{1}{|\mathcal{A}|}\sum_{a'} A(s,a';\theta,\alpha) \right) \]

具体算法：

代码实现

由于只是改动了神经网络的部分架构，我们代码的修改幅度也不大，只要把以前 DQN 中的 _build_net 函数修改一下即可：

def _build_net(self, s, scope, trainable):
    with tf.variable_scope(scope):
        l = tf.layers.dense(s, 20, activation=tf.nn.relu, trainable=trainable, ** initializer_helper)
        v_z = tf.layers.dense(l, 1, trainable=trainable, **initializer_helper)
        a_z = tf.layers.dense(l, self.a_dim, trainable=trainable, **initializer_helper)

        q_z = v_z + a_z - tf.reduce_max(a_z)
    return q_z

查看完整代码，这里只是简单将 double DQN 与 dueling network 进行了结合，还可以加入优先经验回放等其他增强的特性。

参考

Wang, Z., Schaul, T., Hessel, M., Van Hasselt, H., Lanctot, M., & De Freitas, N. (2015). Dueling network architectures for deep reinforcement learning. arXiv preprint arXiv:1511.06581.

Fisher's Blog

Dueling Network Architectures for Deep Reinforcement Learning & 代码实现

Dueling Network 架构

代码实现

参考