Prioritized Experience Replay 介绍了优先经验回放机制，本文将该机制与 Double DQN 进行简单的结合，同时还要介绍在前文中提到的 Sum Tree 数据结构，它能高效的在记忆库中进行基于优先经验回放机制的抽样。直接看代码

Sum Tree

由于使用贪婪法来选取优先经验的时间复杂度太高，同时还有其他问题，所以我们用 \(P(i) =p_i^\alpha / \sum_kp_k^\alpha\) 来定义某个片段的选取概率，其中 \(p_i\) 我们将它等同于 TD-error \(|\delta_i|\) ，并用 Sum Tree 这种数据结构来表示每个存储的片段。

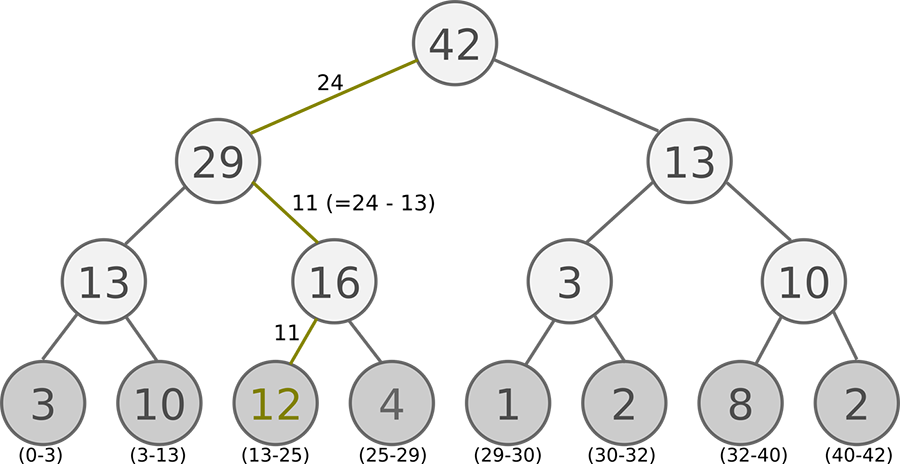
Sum Tree 是一种二叉树类型的数据结构，所有叶子节点存储优先级 \(p_i\) ，所有父节点为子节点之和，所以这棵树的根节点即为所有叶子节点的和，如下图所示：

在抽样时，我们将存储的优先级的个数除以 batch size ，分成 batch size 个区间，如图中的例子，一共有 3, 10, 12, 4, 1, 2, 8, 2 八个优先级节点，如果 batch size = 6 ，那么分成： [0-7], [7-14], [14-21], [21-28], [28-35], [35-42] 六个区间，再分别在六个区间中均匀地随机选择一个数，从根节点依次往下搜索。如在第 4 个区间中选中了 24 ，则将 24 与根节点的左节点进行比较，因为 24 < 29 所以继续往左搜索，将 24 与 29 的左节点比较，发现 24 > 13 ，则继续往右搜索，同时将 24 - 13 = 11 ，将 11 与 16 的左节点比较，11 < 12 ，因为 12 已经是叶子节点，则搜索完毕，选中 12 这个优先级。

图中叶子节点下面括号中的区间代表该优先级可以被搜索到的范围，由此可见优先级大的被搜索到的概率越高，同时优先级小的，也有一定概率被选中。

我们用顺序存储来实现这个二叉树，为了方便，我们规定 sum tree 必须是满二叉树：

class SumTree:
    def __init__(self, capacity):
        # sum tree 能存储的最多优先级个数
        self.capacity = capacity
        # 顺序表存储二叉树
        self.tree = [0] * (2 * capacity - 1)
        # 每个优先级所对应的经验片段
        self.data = [None] * capacity
        self.size = 0
        self.curr_point = 0

    # 添加一个节点数据，默认优先级为当前的最大优先级+1
    def add(self, data):
        self.data[self.curr_point] = data

        self.update(self.curr_point, max(self.tree[self.capacity - 1:self.capacity + self.size]) + 1)

        self.curr_point += 1
        if self.curr_point >= self.capacity:
            self.curr_point = 0

        if self.size < self.capacity:
            self.size += 1

    # 更新一个节点的优先级权重
    def update(self, point, weight):
        idx = point + self.capacity - 1
        change = weight - self.tree[idx]

        self.tree[idx] = weight

        parent = (idx - 1) // 2
        while parent >= 0:
            self.tree[parent] += change
            parent = (parent - 1) // 2

    def get_total(self):
        return self.tree[0]

    # 获取最小的优先级，在计算重要性比率中使用
    def get_min(self):
        return min(self.tree[self.capacity - 1:self.capacity + self.size - 1])

    # 根据一个权重进行抽样
    def sample(self, v):
        idx = 0
        while idx < self.capacity - 1:
            l_idx = idx * 2 + 1
            r_idx = l_idx + 1
            if self.tree[l_idx] >= v:
                idx = l_idx
            else:
                idx = r_idx
                v = v - self.tree[l_idx]

        point = idx - (self.capacity - 1)
        # 返回抽样得到的 位置，transition信息，该样本的概率
        return point, self.data[point], self.tree[idx] / self.get_total()

Memory

class Memory(object):
    def __init__(self, batch_size, max_size, beta):
        self.batch_size = batch_size  # mini batch大小
        self.max_size = 2**math.floor(math.log2(max_size)) # 保证 sum tree 为完全二叉树
        self.beta = beta

        self._sum_tree = SumTree(max_size)

    def store_transition(self, s, a, r, s_, done):
        self._sum_tree.add((s, a, r, s_, done))

    def get_mini_batches(self):
        n_sample = self.batch_size if self._sum_tree.size >= self.batch_size else self._sum_tree.size
        total = self._sum_tree.get_total()
        
        # 生成 n_sample 个区间
        step = total // n_sample
        points_transitions_probs = []
        # 在每个区间中均匀随机取一个数，并去 sum tree 中采样
        for i in range(n_sample):
            v = np.random.uniform(i * step, (i + 1) * step - 1)
            t = self._sum_tree.sample(v)
            points_transitions_probs.append(t)

        points, transitions, probs = zip(*points_transitions_probs)

        # 计算重要性比率
        max_impmortance_ratio = (n_sample * self._sum_tree.get_min())**-self.beta
        importance_ratio = [(n_sample * probs[i])**-self.beta / max_impmortance_ratio
                            for i in range(len(probs))]

        return points, tuple(np.array(e) for e in zip(*transitions)), importance_ratio

    def update(self, points, td_error):
        for i in range(len(points)):
            self._sum_tree.update(points[i], td_error[i])

参考

Schaul, T., Quan, J., Antonoglou, I., & Silver, D. (2015). Prioritized experience replay. arXiv preprint arXiv:1511.05952.

https://morvanzhou.github.io/tutorials/machine-learning/reinforcement-learning/4-6-prioritized-replay/

感谢王健树 StepNeverStop 帮助我理解了 Sum Tree 🙏🙏🙏

Fisher's Blog

Prioritized Experience Replay 代码实现

Sum Tree

Memory

参考