从 基于模型的动态规划之后 一直在介绍无模型 (Model-Free) 的情况,默认了智能体在学习时不知道完整的 MDP ,这也确实是实际学习中绝大多数会遇到的情况,比如我们可以使用 策略梯度 方法直接从经验中学习梯度,又或者直接从经验中学习值函数( 无模型预测 、 无模型控制 )。
本文将再换一个角度,从经验中直接学习我们未知的模型,然后用规划的方法来构造值函数或者策略,将学习与规划整合起来。
基于模型的强化学习 Model-Based Reinforcement Learning
正如在一开始介绍的,基于模型的强化学习就是先从经验中学习模型,再用习得的模型来规划值函数或策略,并不断循环下去。
我们可以高效的通过监督学习 (supervised learning) 的方法来学习模型,在学习了模型之后,智能体不再是一味的追求奖励最大化,还能在一定程度上了解采取的动作为什么是好的或者不好,也就是具备一定的推理能力。 但这样的先学习模型再构造价值函数的两步操作都会有误差,会带来两次近似误差。
什么是模型?
一个模型 \(\mathcal{M}\) 就是一个 MDP \(<\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}>\) 以 \(\eta\) 为参数的参数化表现形式。
我们假设状态空间 \(\mathcal{S}\) 与行为空间 \(\mathcal{A}\) 都是已知的,那么一个模型 \(\mathcal{M} = <\mathcal{P}_\eta ,\mathcal{R}_\eta>\) 代表了状态转移 \(\mathcal{P}_\eta \approx \mathcal{P}\) 和奖励 \(\mathcal{R}_\eta \approx \mathcal{R}\),使得: \[ S_{t+1} \sim \mathcal{P}_\eta(S_{t+1}|S_t,A_t)\\ R_{t+1} = \mathcal{R}_\eta(R_{t+1}|S_t,A_t) \] 通常需要假设状态转移与奖励是条件独立的: \[ \mathbb{P}[S_{t+1},R_{t+1}|S_t,A_t] = \mathbb{P}[S_{t+1}|S_t,A_t] \mathbb{P}[R_{t+1}|S_t,A_t] \]
学习模型
有了以上的定义,我们的目标就是以监督学习的方式,从经验 \(\{S_1,A_1,R_2,\cdots,S_\text{T}\}\) 中学习模型 \(\mathcal{M}_\eta\)
学习奖励 \(s,a \rightarrow r\) 即为回归问题 (regression problem)
学习状态转移 \(s,a \rightarrow s'\) 即为估计概率密度问题 (density estimation problem)
根据监督学习方式的不同,对于模型的选择也可以不同,比如查表式 (Table lookup Model) 、线性期望模型 (Linear Expectation Model) 、线性高斯模型 (Linear Gaussian Model) 、高斯决策模型 (Gaussian Process Model) 、深度信念网络模型 (Deep Belief Network Model) 等。
对于查表式的模型,计算方法如下: \[ \hat{\mathcal{P}^a_{s,s'}} = \frac{1}{N(s,a)} \sum_{t=1}^T 1\{S_t,A_t,S_{t+1}=s,a,s' \} \\ \hat{\mathcal{R}_s^a} = \frac{1}{N(s,a)} \sum_{t=1}^T 1\{ S_t,A_t = s,a \} R_t \] 不过在实际学习中,我们不是以一个回合 (episode) 为单位,而是以 time-step 为单位,将经验片段 \(<S_t,A_t,R_{t+1},S_{t+1}>\) 存储起来,然后随机地抽取片段进行学习。
使用模型进行规划
有了我们估计的模型 \(\mathcal{M}\) 后,就可以使用之前介绍过的值迭代 (value iteration) 、策略迭代 (policy iteration) 进行规划,也可以使用树搜索 (tree search) 方法。
基于采样的规划 Sample-Based Planning
尽管有了估计的模型,理论上可以使用动态规划方法来找到最优价值函数、最优策略,但我们仅仅是利用这个模型来产生一些样本: \[ S_{t+1} \sim \mathcal{P}_\eta(S_{t+1}|S_t,A_t)\\ R_{t+1} = \mathcal{R}_\eta(R_{t+1}|S_t,A_t) \] 然后就像无模型学习一样,只不过现在智能体不是从实际环境中进行学习,而是在我们估计出的模型环境中,利用模型产生的样本来学习。可以使用许多无模型的强化学习算法比如 MC 、 Sarsa 、 Q-learning 。这种基于采样的规划方法通常非常高效。
架构整合
我们将基于模型与不基于模型两种学习整合起来,形成统一的架构,来解决复杂的 MDP 问题。
首先考虑两种经验的来源:
- 真实经验:从环境中采样得来(真实的 MDP ) \[ S' \sim \mathcal{P}^a_{s,s'} \\ R=\mathcal{R}_s^a \]
- 模拟经验:从模型中采样得来(近似的 MDP ) \[ S' \sim \mathcal{P}_\eta(S' |S,A) \\ R = \mathcal{R}_\eta(R|S,A) \] 无模型的强化学习 (Model-Free RL) 就是直接从真实经验中学习 (learn) 价值函数或策略。
基于模型的强化学习 (Model-Based RL) 就是先从真实经验中学习模型,再从模拟的经验中规划 (plan) 价值函数或策略。
Dyna
Dyna 算法将上述两者结合,从真实经验中学习模型,从真实与模拟的经验中学习与规划价值函数或策略。
Dyna-Q 算法如下:

a, b, c, d, e 步都是从实际经验中学习,d 步学习价值函数,e 步学习模型。 f 步的循环则是使用习得的模型来更新价值函数。
基于模拟的搜索 Simulation-Based Search
前向搜索 Forward Search
前向搜索算法通过向前看 (lookahead) 来选择最佳的行为。该算法把当前状态 \(s_t\) 作为根节点来构建一棵搜索树 (search tree) ,用 MDP 的模型来向前看。前向搜索不需要去解决完整的 MDP ,它只需要关注以当前状态开始的子 MDP (sub-MDP) ,以此来解决这个子 MDP
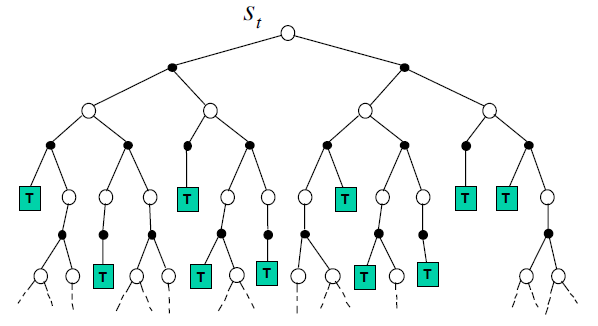
基于模拟的搜索
基于模拟的搜索使用之前介绍的基于采样的规划方法,从当前状态开始,用模型模拟 (simulate) 出一系列的回合经验,然后再将模拟的样本应用到无模型的强化学习方法中。
具体地,从当前状态开始,从模型中采样,生成一系列回合: \[ \{s_t^k,A_t^k,R_{t+1}^k,\cdots, S_T^k \}_{k=1}^K \sim \mathcal{M}_v \] 再用无模型的强化学习方法:
- 蒙特卡罗控制: 蒙特卡罗搜索 (Monte-Carlo search)
- Sarsa : TD 搜索 (TD search)
简单蒙特卡罗搜索 Simple Monte-Carlo Search
给定一个模型 \(\mathcal{M}_v\) 和模拟的策略 \(\pi\)
针对每一个行为 \(a\in\mathcal{A}\) 进行循环:
- 从当前(实际)状态 \(s_t\) 开始,模拟 \(K\) 个回合: \[ \{s_t,a,R_{t+1}^k, S_{t+1}^k,A_{t+1}^k \cdots, S_T^k \}_{k=1}^K \sim \mathcal{M}_v,\pi \]
- 使用平均收获来(蒙特卡罗评估)来评估行为: \[ Q(s_t,a) = \frac{1}{K}\sum_{k=1}^KG_t \stackrel{P}{\longrightarrow} q_\pi(s_t,a) \]
选择最大价值的行为: \[ a_t = \arg\max_{a\in\mathcal{A}} Q(s_t,a) \] 以上就是简单模特卡洛搜索算法的主要思想,它基于一个特定的模拟策略,但如果这个模拟策略本身不是很好的话,那么基于该策略下产生的行为 \(a_t\) 可能就不是状态 \(s_t\) 下的最优行为。考虑另一种搜索算法。
蒙特卡罗树搜索 Monte-Carlo Tree Search
评估 Evaluation
- 给定一个模型 \(\mathcal{M}_v\) ,使用当前的模拟策略 \(\pi\) 从当前状态 \(s_t\) 开始模拟 \(K\) 个回合: \[ \{s_t,A_t^k,R_{t+1}^k, S_{t+1}^k,A_{t+1}^k \cdots, S_T^k \}_{k=1}^K \sim \mathcal{M}_v,\pi \]
- 构建一个包含所有经历过的状态、行为的搜索树
- 用平均收获来评估所有的行为价值函数: \[ Q(s,a) = \frac{1}{N(s,a)} \sum_{k=1}^K \sum_{u=t}^T 1\{S_u,A_u=s,a\} G_u \stackrel{P}{\longrightarrow} q_\pi(s,a) \]
- 当搜索结束后,选择最大价值的行为: \[ a_t = \arg\max_{a\in\mathcal{A}} Q(s_t,a) \] ### 模拟 Simulation
在 MCTS 中,模拟策略 \(\pi\) 需要进行修改。
由于我们没有储存整个 MDP 的行为价值函数,所以每次的模拟要分为两个阶段 (phases),已经存在于搜索树内 (in-tree) 的和树外 (out-of-tree) 的。
- 对于树内部分,采用 Tree policy ,即挑选行为来最大化 \(Q(S,A)\) ,当然也包含一些探索。
- 对于树外部分,采用 Default policy ,即随机选择行为,因为我没有存储任何信息。
在不断的模拟中,用蒙特卡罗来评估行为价值函数,用 ϵ-greedy 来改善 tree policy
这种方法最终将收敛到最优策略 \(Q(S,A) \rightarrow q_*(S,A)\)
在围棋中应用 MCTS
第一次迭代:五角星代表第一次被访问到的状态,也是第一次被录入到搜索树中的状态。我们构建搜索树:首先应用 tree policy 但现在搜索树中只有一个当前状态,所以进入下一阶段,即 default policy ,随机的选择行为,产生一个完整的回合。终止框(方框)中表示黑方获胜,则当前状态记为 1/1 表示从五角星状态开始模拟了一个回合,其中获胜了一个回合。
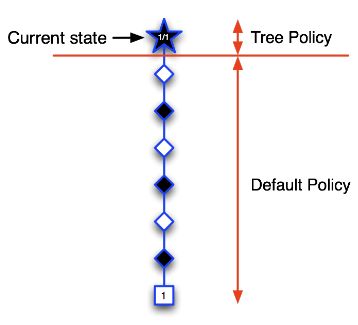
第二次迭代:依然从圆形的当前状态开始模拟,此时 tree policy 中只有一个状态,所以直接选择该五角星状态,将该状态录入搜索树中,继续模拟一个完整的回合。
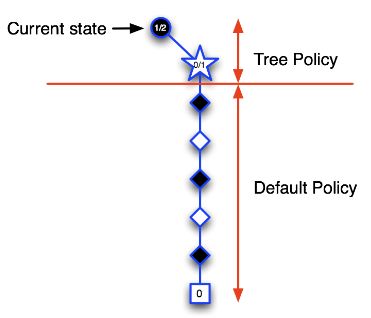
第三次迭代:先以 tree policy 来选择当前状态的下一步行为,假设进入了五角星状态,同样将该状态录入搜索树中,继续模拟一个完整的回合。
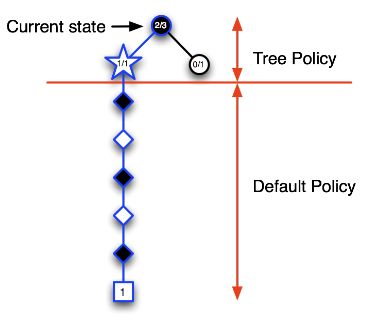
随着迭代次数越来越多,在树内由于使用 ϵ-greedy 选择行为,搜索树会向着最优的路径向前推进,同时对于不怎么好的状态也会有适当的探索。
蒙特卡罗树搜索是具有高度选择性的 (Highly selective) 、基于导致越好结果的行为越被优先选择 (best-first) 的一种搜索方法,与动态规划不同,它可以动态地评估各状态的价值,使用采样避免了维度灾难,也由于采样而适用于那些“黑盒”模型 (black-box models) ,上述这些优点决定了其是可以高效计算、不受时间限制以及可以并行处理。
参考
http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/dyna.pdf

