强化学习的最终目的就是找到 MDP 的最优策略,而在已知模型的情况下,通常用动态规划 (Dynamic Programming) 方法来寻找最优策略。
动态规划是一种非常常见的算法,要应用动态规划方法需要满足两个条件:
- 原本复杂的问题可以被分解成相对简单子问题,求出最优子问题就求出了最优解
- 子问题会反复出现多次,并且子问题的结果可以被存储起来继而解决后续的问题
而 MDP 正好满足了上述两个特性:
- 贝尔曼方程相当于将复杂问题分解为了递归的子问题
- 价值函数相当于存储了之前子问题的解
通过判断一个策略的价值函数,用该策略下的最优价值函数来更新策略并不断重复上述过程直至找到最优价值函数与最优策略便是动态规划的核心思想。
在求解 MDP 的最优策略中使用动态规划一般可以用来:
- 预测:输入 MDP \(<\mathcal{S},\mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma>\) 和策略 \(\pi\) ,或输入 MRP \(<\mathcal{S}, \mathcal{P}^\pi, \mathcal{R}^\pi, \gamma>\) ,输出价值函数 \(v_\pi\)
- 控制:输入 MDP \(<\mathcal{S},\mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma>\) ,输出最优价值函数 \(v_*\) 和最优策略 \(\pi_*\)
策略迭代 Policy Iteration
策略评估 Policy Evaluation
在某个策略 \(\pi\) 下,通过贝尔曼公式,一步步迭代便能评估出这个策略的价值函数 \(v_\pi\) :
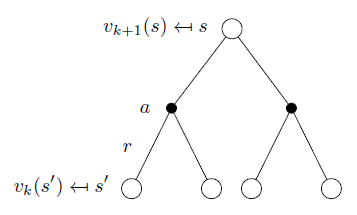 \[
v_{k+1}= \sum_{a\in \mathcal{A}} \pi(a|s)\left( \mathcal{R}^a_s +\gamma\sum_{s'\in\mathcal{S}} \mathcal{P}^a_{ss'}v_k(s') \right)
\] 或用矩阵形式表示: \[
\boldsymbol{v^{k+1}} = \boldsymbol{\mathcal{R}^\pi}+\gamma \boldsymbol{\mathcal{P}^\pi v^k}
\]
\[
v_{k+1}= \sum_{a\in \mathcal{A}} \pi(a|s)\left( \mathcal{R}^a_s +\gamma\sum_{s'\in\mathcal{S}} \mathcal{P}^a_{ss'}v_k(s') \right)
\] 或用矩阵形式表示: \[
\boldsymbol{v^{k+1}} = \boldsymbol{\mathcal{R}^\pi}+\gamma \boldsymbol{\mathcal{P}^\pi v^k}
\]
策略更新 Policy Improvement
上一节的策略评估只是预测出了某一个策略下的价值函数,评估以后我们还需要用评估的结果来改进策略。所以策略迭代 (policy iteration) 做了两件事:给定一个策略 \(\pi\)
- 评估策略 \(v_\pi(s) = \mathbb{E}[R_{t+1}+\gamma R_{t+2} + \cdots|S_t=s]\)
- 用贪婪法改进策略 \(\pi' = \text{greedy}(v_\pi)\)
并不断重复以上两个过程,直至算法收敛。
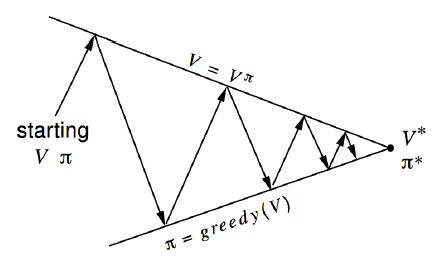
图中可以看出给定一个策略,箭头往上表示策略评估,评估完毕箭头往下表示策略改进,直至收敛。
那么如何用贪婪法来改进策略呢?假设现在考虑确定性策略 \(a=\pi(s)\) ,我们可以贪婪地更新策略: \[ \pi'(s)=\arg\max_{a\in\mathcal{A}} q_\pi(s,a) \] 可以证明这种策略改进的方法确实是朝更好的方向进行的。如果这种更新停止了,那么也就表示满足了贝尔曼最优方程: \[ q_\pi(s,\pi'(s)) = \max_{a\in\mathcal{A}}q_\pi(s,a)=q_\pi(s,\pi(s)) = v_\pi(s) \] 即对于所有的 \(s\in\mathcal{S}\) 都有 \(v_\pi(s) = v_*(s)\) ,\(\pi\) 也就是最优策略。
价值迭代 Value Iteration
一个最优策略可以分为两部分:
- 每一步的行动都采取了最优行动 \(A_*\)
- 下一个状态 \(s'\) 也遵循最优策略
而一个策略能使状态 \(s\) 达到最优价值 \(v_\pi(s) = v_*(s)\) 必须要满足:
- 从状态 \(s\) 可以到达任意状态 \(s'\)
- 该策略能够使得状态 \(s'\) 的价值是最优价值:
以上就是优化原则 (Principle of Optimality) ,如果我们能够知道最优子问题的解 \(v_*(s')\) ,就可以根据贝尔曼最优方程直接求解最优价值函数,一步到位: \[ v_*(s) \leftarrow \max_{a\in\mathcal{A}} \bigg(\mathcal{R}_s^a + \gamma \sum_{s'\in \mathcal{S}}{\mathcal{P}_{ss'}^a v_*(s')}\bigg) \]
小结
本文介绍了三种应用动态规划解决的问题:
| 问题 | 贝尔曼方程 | 算法 |
|---|---|---|
| 预测 | 贝尔曼期望方程 | 迭代法策略评估 |
| 控制 | 贝尔曼期望方程 + 贪婪策略 | 策略迭代 |
| 控制 | 贝尔曼最优方程 | 价值迭代 |
在实际强化学习过程中,已知模型的情况非常少,很少使用动态规划方法来解决问题。
参考
http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/DP.pdf

