在已知模型的情况下,可以用动态规划方法解决 MDP 问题,但在强化学习中,更多遇到的是无模型情况 (Model-Free) ,也就是模型 \(P^a_{ss'}\) 是未知的,比如一架直升机处于 \(s\) 状态,在采取动作 \(a\) 之后,我们不知道有多大概率会转移到 \(s'\) 状态,当时的环境状况会产生很大的干扰。
本文就是要在在未知模型的情况下,估计价值函数,包括蒙特卡罗方法与时间差分方法。
蒙特卡罗方法 Monte-Carlo
蒙特卡罗 (MC) 方法直接从一次次的回合 (episode) 的经验之中进行学习,这一次次的回合都是完整的回合,所以不需要自举 (bootstrapping) ,同时也就意味着每一个回合有回合的开始也必须有回合的结束。
蒙特卡罗平均值法求期望
在数学上,经常会遇到求期望的问题,比如设 \(X\) 服从 \([0,1]\) 上的均匀分布,则 \(Y=f(X)\) 的期望为: \[ \mathbb{E}[f(X)] = \int_0^1 f(x) \mathrm{d}x \] 根据辛钦大数定理(弱大数定理):设 \(X_1, X_2, \cdots\) 是独立同分布的随机变量序列,且具有数学期望 \(\mathbb{E}[f(X)] = \mu\) ,作前 n 个变量的算术平均 \(\frac{1}{n}\sum_{k=1}^n f(X_k)\) ,则对于任意 \(\varepsilon >0\) ,有 \[ \lim_{n \rightarrow \infty} P\left\{ \left| \frac{1}{n}\sum_{k=1}^n f(X_k) - \mu \right| <\varepsilon \right\}=1 \] 也就是说 \(\overline{X} = \sum_{k=1}^n f(X_k)\) 依概率收敛于 \(\mu\) 。
MC 的思想非常简单,产生服从 \([0,1]\) 均匀分布的随机数字 \(X_1,X_2,\cdots\) ,对每一个数字计算 \(f(X_i)\) ,并求出均值则可以近似的表示为 \(f(X)\) 的期望。
回到强化学习上,我们的目标就是根据策略 \(\pi\) 生成一系列的回合 \(S_1,A_1,R_1,\cdots,S_k \sim \pi\) ,从经验中学习价值函数 \(v_\pi\) ,总回报是 \(G_t = R_{t+1}+\gamma R_{t+2} + \cdots + \gamma^{\text{T}-1} R_\text{T}\) ,而我们的价值函数就是总回报的期望 \(v_\pi(s) = \mathbb{E}_\pi[G_t|S_t=s]\) ,相当于环境根据某个分布 \(\pi\) 自动产生了一系列随机回报数字,要求的就是这些数字的经过处理之后的 \(G_t\) 的期望。这就可以使用 MC ,用 MC 的经验平均 (empirical mean) 回报来代替期望回报。
首次访问蒙特卡罗策略评估 First-Visit MC Policy Evaluation
在一个完整的回合之中,首次出现状态 \(s\) 时计算:
- 状态出现次数加一:\(N(s) \leftarrow N(s) +1\)
- 总回报更新:\(S(s) \leftarrow S(s) + G_t\)
- 价值函数根据均值更新:\(V(s) = S(s) / N(s)\)
- 当回合数试验地非常多时,即当 \(N(s) \rightarrow \infty\) 时, \(V(s) \rightarrow v_\pi(s)\)
每次访问蒙特卡罗策略评估 Every-Visit MC Policy Evaluation
与 首次访问蒙特卡罗策略评估 算法相同,只不过在一个完整的回合中,每次出现状态 \(s\) 就进行计算,因为回合中可能多次出现同一状态:
- 状态出现次数加一:\(N(s) \leftarrow N(s) +1\)
- 总回报更新:\(S(s) \leftarrow S(s) + G_t\)
- 价值函数根据均值更新:\(V(s) = S(s) / N(s)\)
- 当回合数试验地非常多时,即当 \(N(s) \rightarrow \infty\) 时, \(V(s) \rightarrow v_\pi(s)\)
累进平均 Incremental Mean
在求均值时,根据公式会把所有 \(x_j\) 保留下来,再累加之和除以总数。在实际中可以用累进平均的小技巧来求得平均值: \[ \begin{align*} \mu_k &= \frac{1}{k}\sum_{j=1}^k x_j \\ &= \frac{1}{k} \left( x_k+\sum_{j=1}^{k-1} x_j \right) \\ &= \frac{1}{k} (x_k+(k-1)\mu_{k-1}) \\ &= \mu_{k-1} + \frac{1}{k}(x_k-\mu_{k-1}) \end{align*} \] 这样就不需要将所有的 \(x_j\) 都保存在内存里,节省内存空间。
蒙特卡罗累进更新 Incremental Monte-Carlo Updates
在每一个回合完成之后就进行 \(V(s)\) 的更新:对每一个状态 \(S_t\) 和 回报 \(G_t\) : \[ \begin{align*} N(S_t) &\leftarrow N(S_t) + 1 \\ V(S_t) &\leftarrow V(S_t) + \frac{1}{N(S_t)}(G_t - V(S_t)) \end{align*} \] 在处理非静态问题 (non-stationary) 时,用这种方法来获得均值非常有用,可以抛弃之前的回合信息,引入参数 \(\alpha\) 来更新状态: \[ V(S_t) \leftarrow V(S_t) + \alpha(G_t - V(S_t)) \]
时间差分学习 Temporal-Difference Learning
与 MC 相同,时间差分 (TD) 方法也无模型的、直接从回合经验中进行学习,但与 MC 不同的是 TD 算法可以从不完整的回合中通过自举 (bootstrapping) 进行学习,通过一个猜测来更新另一个猜测。
MC 中需要完整的回合是因为要用实际总回报 \(G_t\) 更新价值函数,即 \(V(S_t) \leftarrow V(S_t) + \alpha(\boldsymbol{G_t} - V(S_t))\) ,但最简单的 TD(0) 算法是根据估计的回报 \(R_{t+1} + \gamma V(S_{t+1})\) 来更新价值函数,即: \[ V(S_t) \leftarrow V(S_t) + \alpha(\boldsymbol{ R_{t+1} + \gamma V(S_{t+1}) } - V(S_t)) \] 其中 \(R_{t+1} + \gamma V(S_{t+1})\) 称为 TD 目标 (TD target) ,\(\delta_t=R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\) 称为 TD 误差 (TD error)
MC vs. TD
- TD 可以在知道回合结果之前就进行学习
- MC 必须等到回合结束,并已知回合的总回报
- TD 可以在没有终止状态的连续环境中学习不完整的回合
- MC 必须在有终止状态的环境中学习完整的回合序列
回报 \(G_t\) 是 价值函数 \(v_\pi(S_t)\) 的无偏估计 (unbiased estimate) True TD target \(R_{t+1} + \gamma v_\pi(S_{t+1})\) 是 \(v_\pi(S_t)\) 的无偏估计 TD target \(R_{t+1} + \gamma V(S_{t+1})\) 是 \(v_\pi(S_t)\) 的有偏估计 (biased estimate) TD target 比回报有着更小的方差 (variance) ,因为回报依赖于许多随机的行为、状态转移和奖励,而TD target 只依赖与一次随机行为、状态转移和奖励,因此:
- MC 有着较高的方差、零偏差,有很好的收敛特性(即使对于后面章节中的近似函数来说),对初始值不敏感,容易使用
- TD 有着较小的方差、一些偏差,比 MC 更加高效,TD(0) 可以收敛到 \(v_\pi(s)\) 但对于近似函数来说则不一定,对初始值更敏感
- TD 利用了马尔可夫性 (Markov property) ,在马尔可夫环境中更有效
- MC 没有用到马尔可夫性,在非马尔科夫环境中更有效
三张图可以直观的看出 MC 、 TD(0) 与 DP 的区别:
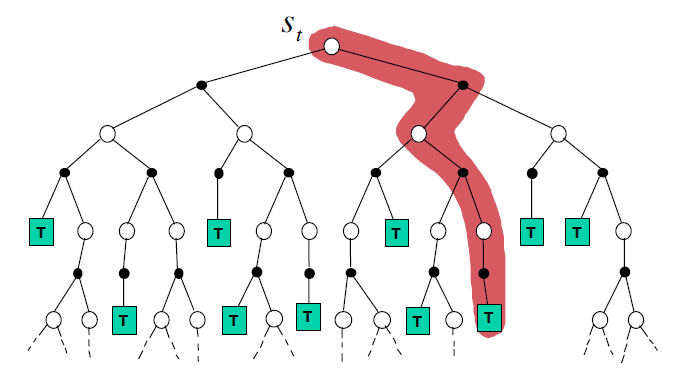
Monte-Carlo Backup :需要采样,不自举,需要一个完整的回合(图中从根节点到叶结点 T 的一条路径就是一个回合) \[
V(S_t) \leftarrow V(S_t) + \alpha(G_t - V(S_t))
\] 
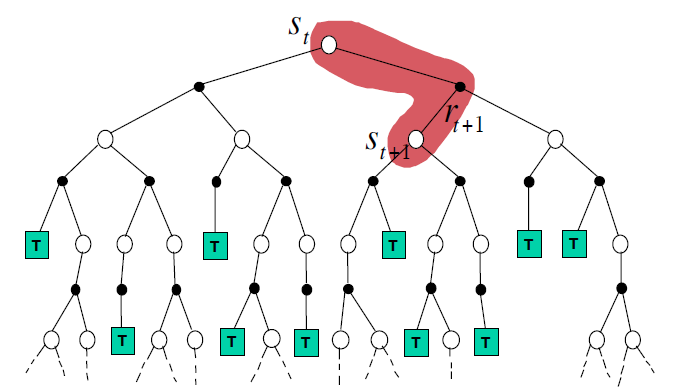
Temporal-Difference Backup :需要采样,自举,只需要向前走一次 \[
V(S_t) \leftarrow V(S_t) + \alpha(R_{t+1}+\gamma V(S_{t+1}) - V(S_t))
\] 
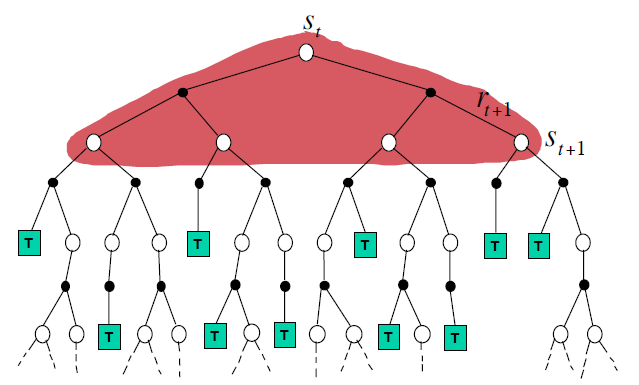
Dynamic Programming Backup :没有采样,自举,但需要完整的模型 \[
V(S_t) \leftarrow \mathbb{E}_\pi[R_{t+1} + \gamma V(S_{t+1})]
\] 
TD(λ)
上文介绍了最简单的 TD(0) ,即只在当前状态下,往前走一步,看一看下一次的状态,计算回报。那如果往前走 n 步呢?定义 n 步的回报: \[ G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n v(S_{t+n}) \] 可以看出,如果 \(n=1\) ,即只向前走一步,就是 TD(0) ,而如果 \(n \rightarrow \infty\) 就是 MC 。走 n 步的 TD 算法为: \[ V(S_t) \leftarrow V(S_t) + \alpha \left( G_t^{(n)} - V(S_t) \right) \] 注:尽管上文一直提到 TD(0) ,但这里的 0 代表的参数 λ ,与走 n 步无关,参数 λ 会在下文进行介绍。
我们可以将 n 步的回报根据不同的 n 平均一下,比如平均 2 步和 4 步的回报: \[ \frac{1}{2}G^{(2)} + \frac{1}{2}G^{(4)} \] 现引入参数 λ 来高效地整合所有步数产生的回报:定义 λ-回报 (λ-return) \(G^\lambda_t\) 结合了所有步数的回报值 \(G_t^{(n)}\) ,使用权重 \((1-\lambda)\lambda^{n-1}\) 来平均回报: \[ G_t^\lambda = (1-\lambda) \sum_{n=1}^\infty \lambda^{n-1} G_t^{(n)} \qquad \lambda\in[0,1] \] 注意到 \((1-\lambda)\sum_{n=1}^\infty \lambda^{n-1} = 1\) ,每步的权重程衰减的趋势。
以此,定义 TD(λ) 算法: \[ V(S_t) \leftarrow V(S_t) + \alpha \left( G_t^\lambda - V(S_t) \right) \] 可以发现,当 \(\lambda = 0\) 时,即 TD(0) 算法,后一步的权重最大为 1 ,其余都为 0 。而 \(\lambda = 1\) 时,即为 MC 算法。
前向视角 Forward-view TD(λ)
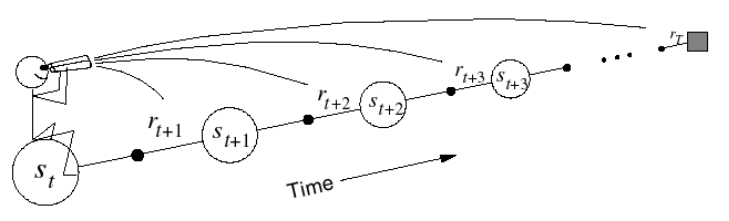
对于前向视角,如果要更新一个状态的状态价值,就必须要走完整个回合,再通过 TD(λ) 算法,施加一些权重,像图里的小人坐在开始状态向前看未来的状态与回报。这与 MC 算法的要求一样,与 MC 有着相同的缺点,给计算带来不便。
反向视角 Backward-view TD(λ)
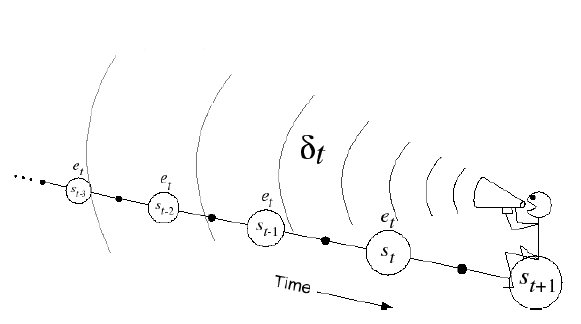
从图中能看出在反向视角中,要更新当前状态,与之前的状态、奖励有关,而不需要去看未来的状态。
资格迹 Eligibility Traces
先举个例子,若一只老鼠在连续接受了3次响铃和1次亮灯信号后遭到了电击,那么遭电击的原因是因为最近的一次亮灯还是最频繁的三次响铃呢? 这是两种不同的观点:
- 频率启发 Frequency heuristic:将原因归因于出现频率最高的状态
- 就近启发 Recency heuristic:将原因归因于最近出现的几次状态
资格迹结合了这两种观点: \[ \begin{align*} E_0(s) &= 0 \\ E_t(s) &= \gamma \lambda E_{t-1}(s)+ 1\{S_t=s\} \end{align*} \] 后向视角的 TD(λ) 算法为: \[ \delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \\ V(s) \leftarrow V(s) + \alpha \delta_t E_t(s) \] 当 \(\lambda=0\) 时,只有当前状态被更新: \[ E_t(s) = 1\{ S_t=s \} \\ V(s) \leftarrow V(s) + \alpha \delta_t E_t(s) \] 与 TD(0) 算法等价: \[ V(s_t) \leftarrow V(s_t) + \alpha \delta_t \] 当 \(\lambda = 1\) 时,反向视角也就是使用在线更新,粗略的看起来,与 every-visit MC 算法相同,状态价值会一步步累积起来,若在回合结束之后再去计算价值函数,也就是离线更新,则与 MC 算法完全相同。
前向视角与后向视角的 TD(λ) 在更新总量上相等。
一张图总结一下前向视角与后向视角 TD(λ) 的异同
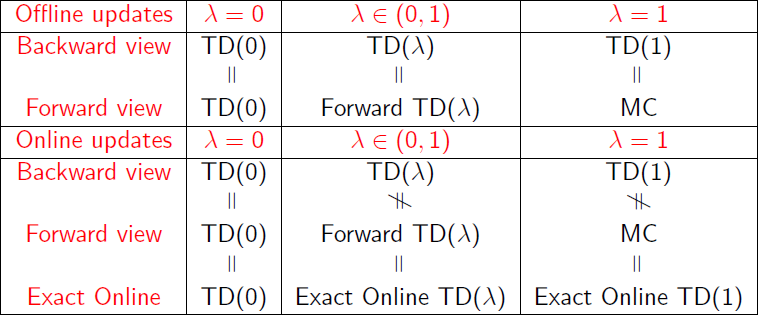
如果使用离线更新,也就是等待回合完成,则两种视角完全相同。但如果是在线更新方式,两种视角有些小许不同。
参考
http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/MC-TD.pdf

