DeepMind 在 Distributed Prioritized Experience Replay 的基础上增加了 RNN 的支持,于是形成了本文要介绍的论文 Recurrent Experience Replay in Distributed Reinforcement Learning 。论文主要讨论了由于使用经验池机制产生参数滞后 (parameter lag) 现象而导致的表征漂移 (representational drift) 和 RNN 隐藏状态滞后 (recurrent state staleness) 问题,这两个问题在分布式学习中更加显著。
Background
首先简单介绍下论文的背景。
Reinforcement Learning
本文不再赘述强化学习中 MDP 和 POMDP 的定义。需要注意的是,DQN 算法是使用 4 个连续帧作为状态输入,使用经验池机制来训练 Q 网络。其他算法如 A3C 等可以使用 LSTM ,但是直接训练一个轨迹,没有用到经验池。Deep recurrent Q-learning for partially observable MDPs 将 DQN 与 LSTM 结合起来,在经验池中储存一个序列,在训练时 RNN 的初始状态为零。
Distributed Reinforcement Learning
主要分为 Ape-X 和 IMPALA 两个算法,Ape-X 用到了经验池,IMPALA 则是使用先进先出的队列,同时采用了一个新颖的 off-policy 修正算法:V-trace 。
The Recurrent Replay Distributed DQN Agent
论文主要提出了一种新的智能体 Recurrent Replay Distributed DQN (R2D2) ,使用它来研究 RNN 状态,经验池与分布式学习之间的关系。R2D2 与 Ape-X 非常类似,都是基于优先经验回放机制和 n-step double Q-learning (n=5) ,由大规模数量的 actors (一般 256 个) 生成经验,并由一个单独的学习器从经验池中采集数据学习。
相较于传统经验池中储存的是 \((s,a,r,s')\) ,作者储存固定长度 (\(m=80\)) 的 \((s,a,r)\) 序列,且相邻序列相互重叠40步,不超过一个轨迹的边界。
与 Ape-X 不同的是,作者参考了 Observe and Look Further: Achieving Consistent Performance on Atari 这篇论文,将 Q 函数用 \(h(x)=\operatorname{sign}(x)(\sqrt{|x|+1}-1)+\epsilon x\) 压缩,即: \[ \hat{y}_{t}=h\left(\sum_{k=0}^{n-1} r_{t+k} \gamma^{k}+\gamma^{n} h^{-1}\left(Q\left(s_{t+n}, a^{*} ; \theta^{-}\right)\right)\right), \quad a^{*}=\underset{a}{\arg \max } Q\left(s_{t+n}, a ; \theta\right) \] 优先经验回放中的优先值与 Ape-X 也有不同,作者混合了 n-step TD-errors \(\delta_i\) 的最大与平均值 \(p=\eta \max _{i} \delta_{i}+(1-\eta) \overline{\delta}\) 。
Training Recurrent RL Agents with Experience Replay
在 Deep recurrent Q-learning for partially observable MDPs 论文中,作者比较了两种使用经验池机制训练 LSTM 的方法:
- 在从经验池采样得到的序列开头,使用全零状态初始化网络。这种方式的好处在于它的简单性,它可以将互相之间有关联的短序列独立化、去关联化。但另一方面,它又会迫使 RNN 学习从无意义的初始状态中恢复有意义的状态预测,这限制了 RNN 对长时记忆的能力。
- 回放整个完整的轨迹。这种方法避免了需要找一个最佳 RNN 初始值的问题,但会带来计算量、实现上的复杂问题,同时也会带来高方差问题,因为网络的更新依赖于完整的有关联的轨迹序列而不是从经验池中采样得到的无关联序列。
但在该论文中,由于是用 Atari 来做实验,作者发现这两种方法之间的差异不明显,所以使用了更简单的第一种方法。 一种解释是在某些情况下 RNN 在一定数量的 burn-in (烤机) 步后,可以收敛到一个更加合理的 RNN 隐藏状态,因此可以在一个足够长的序列中,RNN 可以从一个差的状态恢复。也有可能是因为实验环境的关系,Atari 游戏相对而言它的观测值是比较全面的,而 DMLab 则是完全与要靠长时记忆来完成。
为了解决这些问题,作者提出了两种方法来训练从经验池中随机采样序列的 RNN 方法,它们可以单独使用,也可以合起来使用。
- Stored state:将 RNN 的隐藏状态储存在经验池中,并以此在训练阶段初始化 RNN 网络。这种方法在一定程度上解决的全零初始状态的问题,但会带来表征漂移 (representational drift) 新问题,使得 RNN 隐藏状态滞后 (recurrent state staleness) ,因为储存的状态可能会明显落后于最近更新过的 RNN 网络。
- Burn-in:先将从经验池中采样得到的序列的一部分用来产生 RNN 的初始状态,剩余的序列部分再在这个初始状态的基础上更新 RNN 网络。作者认为这种方法可以让 RNN 网络从一个比较差的初始状态(如全零或储存的滞后状态)中恢复出一个较好的初始状态。
在论文的实验中,作者采用了长度 \(m=80\) 的经验序列,可选的 burn-in 长度为 \(l=40\) 或 \(l=20\) 步。论文主要比较了在训练过程中表征漂移与 RNNR 状态滞后现象所带来的影响,为了达到这个目的,作者比较了两种生成 Q 值的方式(下图绿色框表示从经验池中采样得到的一个序列):
- (下图红线)使用经验池序列来产生的 Q 值,即经验池中储存 RNN 的初始状态 \(h_t\) 或者用全零状态代替和观测值 \(o_t, \cdots, o_{t+m}\) ,Q 值通过上述提到的 stored state 和 burn-in 方法生成,用 \(\hat{h}_{t}\) 表示,初始状态为 \(\hat{h}_{t}=0\) 或 \(\hat{h}_{t}=h_{t}\)。
- (下图蓝线)直接使用储存在经验池中的 RNN 状态产生的 Q 值。即经验池中需要储存 \(o_t, \ldots, o_{t+m}\) 和 \(h_{t}, \ldots, h_{t+m}\) 。
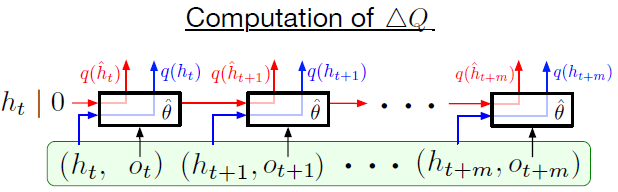
计算表征漂移与 RNN 状态滞后现象公式为: \[ \Delta Q=\frac{\left\|q\left(\hat{h}_{t+i} ; \hat{\theta}\right)-q\left(h_{t+i} ; \hat{\theta}\right)\right\|_{2}}{\left|\max _{a, j}\left(q\left(\hat{h}_{t+j} ; \hat{\theta}\right)\right)_{a}\right|} \]
实验只比较了经验池序列的第一个 \(i=l\) 与最后一个 \(i=l+m-1\) 的 Q 值。下图为在 DMLab 下的实验结果:
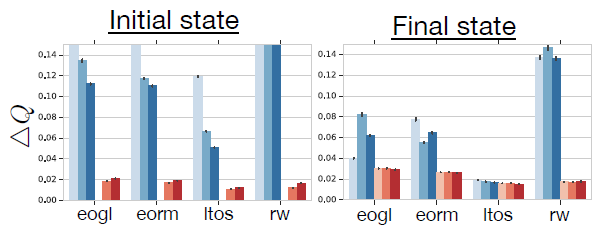
可以发现全零初始状态更可能导致 RNN 网络的滞后性,但相对于序列中的第一个状态,最后一个状态的滞后性影响更小,也就是说 RNN 可能需要一定的时间来从无意义的初始状态中恢复,但仍然比使用 stored state 方法滞后性更明显一点。 同时 burn-in 方法在一定程度上减缓了 RNN 状态滞后性,但随着序列的增加,这种影响变得不怎么明显。下图展示了使用不同方法的累积期望回报:
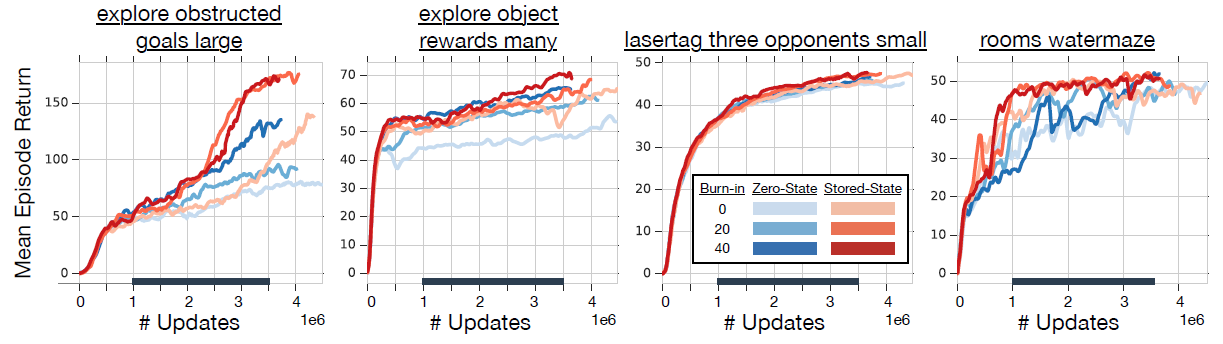
从这些实验结果也可以得出结论:stored state 和 burn-in 方法相对于全零初始状态而言具有更好的性能。
参考
Kapturowski, S., Ostrovski, G., Quan, J., Munos, R., & Dabney, W. (2018). Recurrent experience replay in distributed reinforcement learning.

