深度强化学习在一系列任务中取得了显着的成功,从机器人的连续控制问题到 Go 和 Atari 等游戏。 但到目前为止,深度强化学习的发展在这些领域中仅局限于单个任务,每个智能体需要对每个任务进行单独的调整和训练。
DeepMind 开发了一套新的训练环境,DMLab-30,在具有相同的动作空间和图像状态环境中进行各种各样的挑战。

而 DeepMind 在 Impala: Scalable distributed deep-rl with importance weighted actor-learner architectures 论文中,只用一个智能体在多个任务上进行学习。为了训练智能体在多任务上获得更好的效果,需要大吞吐量并能有效利用每个数据点。 为此,DeepMind 开发了一种新的,高度可扩展的分布式体系结构,称为 Importance Weighted Actor-Learner Architecture,它使用一种称为 V-trace 的 off-policy 校正算法。
Introduction
Importance Weighted Actor-Learner Architecture (IMPALA) 可以扩展到数千台机器,而不会牺牲训练稳定性或数据利用率。与基于 A3C 的智能体 (每一个线程会与中心策略参数服务器进行梯度通信)不同,IMPALA 中的 actors 会将经验轨迹(状态、动作和奖励序列)传达给中心 learner 。由于 learner 可以获得完整的经验轨迹,因此作者使用 GPU 在小批量轨迹上进行训练更新,同时并行化所有时间独立的操作。这种类型的解耦结构可以实现非常高的吞吐量。但是,由于 actor 用于生成轨迹的策略可能会在 learner 进行梯度计算时落后于 learner 多次更新后的策略,因此这种训练方式变成 off-policy ,作者引入了 V-trace 用于纠正这种 off-policy actor-critic 算法。
在使用了这个可伸缩性框架与 V-trace 后,IMPALA 可以以非常高的吞吐量在一秒内处理 250000 帧的图像,比在单台机器上的 A3C 快 30 倍。最关键的是,IMPALA 比 A3C 对于数据利用率更加高效,同时对神经网络结构和参数更加鲁棒。
IMPALA
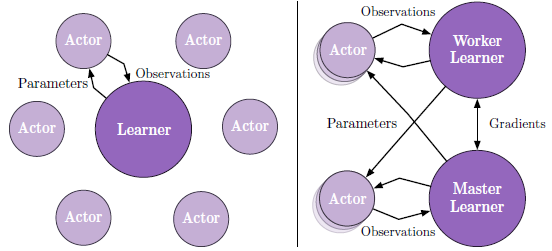
上图使用了 actor-critic 的架构设置来学习策略 \(\pi\) 和基准函数 \(V^\pi\) 。生成轨迹的过程与学习参数的过程解耦。IMPALA 由多个 actors 组成,重复地生成经验轨迹,同时一个或多个 learner 使用这些经验来 off-policy 地学习 \(\pi\) 。上图为 IMPALA 的两种架构,左图使用了一个 learner,每一个 actor 生成轨迹,并通过队列传递给 learner,在下一个回合之前,actor 从 learner 更新策略参数。右图使用了多个同步 learner,策略参数由多个 learner 同步更新和存储。
在每个轨迹的一开始,actor 将它自身的本地策略 \(\mu\) 更新为最新的 learner 策略 \(\pi\) 并与环境交互 \(n\) 次。之后再把状态、动作和奖励轨迹 \(x_{1}, a_{1}, r_{1}, \ldots, x_{n}, a_{n}, r_{n}\) 与相对应的策略分布 \(\mu\left(a_{t} | x_{t}\right)\) 和 LSTM 的初始状态传递给队列中。Learner 持续地根据轨迹按批更新它的策略 \(\pi\) 。但 learner 的策略 \(\pi\) 会在更新的过程中超前 actor 的策略 \(\mu\) ,造成 learner 与 actor 之间的策略滞后 (policy-lag) 。
V-trace
考虑这样一个由 actor 根据某个策略 \(\mu\) 生成的轨迹 \(\left(x_{t}, a_{t}, r_{t}\right)_{t=s}^{t=s+n}\) ,我们定义在状态 \(x_s\) 处,对于 \(V(x_s)\) 的 n-steps V-trace target 价值估计,为: \[ v_{s} \stackrel{\mathrm{def}}{=} V\left(x_{s}\right)+\sum_{t=s}^{s+n-1} \gamma^{t-s}\left(\prod_{i=s}^{t-1} c_{i}\right) \delta_{t} V \tag{1} \] 其中 \(\delta_{t} V \stackrel{\mathrm{def}}{=} \rho_{t}\left(r_{t}+\gamma V\left(x_{t+1}\right)-V\left(x_{t}\right)\right)\) 是 \(V\) 的时间差分,\(\rho_{t} \stackrel{\mathrm{def}}{=} \min \left(\overline{\rho}, \frac{\pi\left(a_{t} | x_{t}\right)}{\mu\left(a_{t} | x_{t}\right)}\right)\) 、\(c_{i} \stackrel{\mathrm{def}}{=} \min \left(\overline{c}, \frac{\pi\left(a_{i} | x_{i}\right)}{\mu\left(a_{i} | x_{i}\right)}\right)\) 为截断的重要性采样权重 (truncated importance sampling weights) ,当 \(s=t\) 时,我们定义 \(\prod_{i=s}^{t-1} c_{i}=1\) ,另外我们假设 \(\overline{\rho} \geq \overline{c}\) 。
如果是 on-policy 情况下 (\(\pi=\mu\)) ,假设 \(\overline{c} \geq 1\) ,那么所有的 \(c_{i}=1\) ,\(\rho_{t}=1\) ,公式 1 可以重写为: \[ \begin{aligned} v_{s} &=V\left(x_{s}\right)+\sum_{t=s}^{s+n-1} \gamma^{t-s}\left(r_{t}+\gamma V\left(x_{t+1}\right)-V\left(x_{t}\right)\right) \\ &=\left[ \sum_{t=s}^{s+n-1} \gamma^{t-s} r_{t} \right] +\gamma^{n} V\left(x_{s+n}\right) \end{aligned} \] 即为标准的 on-policy n-steps Bellman target。因此在 on-policy 情况下,V-trace 会衰减到 on-policy n-steps Bellman update。
公式 1 中的截断重要性采样权重 \(c_i\) 与 \(\rho_i\) 有不同的作用。
\(\rho_i\) 只出现在时间差分 \(\delta_{t} V\) 中,定义了这个更新规则的不动点。 在表格形式下,值函数不需要近似,可以完全被表示( \(V(x_s)=v_s\) ,即 \(\delta_{t} V=0\) ),那么这个更新的不动点是一个值函数 \(V^{\pi_{\overline{\rho}}}\) ,这个值函数对应某个策略 \(\pi_{\overline{\rho}}\) : \[ \pi_{\overline{\rho}}(a | x) \stackrel{\mathrm{def}}{=} \frac{\min (\overline{\rho} \mu(a | x), \pi(a | x))}{\sum_{b \in A} \min (\overline{\rho} \mu(b | x), \pi(b | x))} \] 所以当 \(\overline{\rho}\) 无限大时,这个不动点为目标策略的值函数 \(V^{\pi}\) ,对应的策略 \(\pi\) 为: \[ \pi(a|x) = \frac{\pi(a|x)}{\sum_{b\in A}\pi(b|x)} \] 如果 \(\overline{\rho}\) 不是无限大时,这个值函数 \(V^{\pi_{\overline{\rho}}}\) 不动点所对应的策略 \(\pi_{\overline{\rho}}\) 在 \(\mu\) 与 \(\pi\) 之间,当 \(\overline{\rho}\) 接近零,不动点变为 \(V^\mu\) 。
对于乘积 \(c_{s} \ldots c_{t-1}\) ,它们衡量了 t 时刻的时间差分 \(\delta_{t} V\) 如何影响之前 s 时刻价值函数的更新。\(\pi\) 与 \(\mu\) 越不相同,这个乘积的方差就越大,作者使用了截断 \(\overline{c}\) 来降低方差,但并不影响收敛到哪个价值函数上,因为这只与 \(\overline{\rho}\) 有关。
总结一下, \(\overline{\rho}\) 影响收敛到的价值函数是更靠近 \(\pi\) 策略还是更靠近 \(\mu\) 策略, \(\overline{c}\) 影响收敛的速度。
备注 1. V-trace targets 可以递归地计算: \[ v_{s}=V\left(x_{s}\right)+\delta_{s} V+\gamma c_{s}\left(v_{s+1}-V\left(x_{s+1}\right)\right) \] 备注 2. 我们可以引入一个衰减因子 \(\lambda\in[0,1]\) :\(c_{i}=\lambda \min \left(\overline{c}, \frac{\pi\left(a_{i} | x_{i}\right)}{\mu\left(a_{i} | x_{i}\right)}\right)\) 。在 on-policy 情况下,\(n=\infty\) 时,V-trace 就是 \(TD(\lambda)\)。
V-trace Actor-critic Algorithm
考虑参数化的价值函数 \(V_\theta\) 与当前策略 \(\pi_w\) ,actors 根据行为策略 \(\mu\) 生成轨迹,V-trace targets \(v_s\) 由公式 1 定义。在训练的 \(s\) 时刻,价值参数 \(\theta\) 通过最小化 \(V_\theta(x_s)\) 与 \(v_s\) 之间的 l2 loss ,朝着如下方向更新: \[ \left(v_{s}-V_{\theta}\left(x_{s}\right)\right) \nabla_{\theta} V_{\theta}\left(x_{s}\right) \] 策略参数 \(w\) 朝如下方向更新: \[ \rho_{s} \nabla_{\omega} \log \pi_{\omega}\left(a_{s} | x_{s}\right)\left(r_{s}+\gamma v_{s+1}-V_{\theta}\left(x_{s}\right)\right) \] 为了避免过早收敛,我们可以像 A3C 一样在梯度方向上加上 entropy bonus: \[ -\nabla_{\omega} \sum_{a} \pi_{\omega}\left(a | x_{s}\right) \log \pi_{\omega}\left(a | x_{s}\right) \]
V-trace 与 \(Q^\pi (\lambda)\) , Retrace(\(\lambda\)) 比较
V-trace 是基于 Safe and efficient off-policy reinforcement learning 一文中的 Retrace(\(\lambda\)) 算法,而 Retrace(\(\lambda\)) 又是基于 Q(\(\lambda\)) with Off-Policy Corrections 中的 \(Q^\pi (\lambda)\) 算法,本小节简单整理一下这三个算法的演进路线。
Q(\(\lambda\)) with Off-Policy Corrections: \(Q^\pi (\lambda)\)
给定一个目标策略 \(\pi\) ,和一个生成回报的行为策略 \(\mu\) ,定义 off-policy corrected return operator 操作 \(\mathcal{R}^{\pi, \mu}\) :估计一种回报,该回报应该是由策略 \(\pi\) 生成的,同时使用当前 \(Q^\pi\) 的估计 \(Q\) 来修正。 \[ \left(\mathcal{R}^{\pi, \mu} Q\right)(x, a) \stackrel{\operatorname{def}}{=} r(x, a)+\mathbb{E}_{\mu}\left[\sum_{t \geq 1}^{\top} \gamma^{t}\left(r_{t}+\mathbb{E}_{\pi} Q\left(x_{t}, \cdot\right)-Q\left(x_{t}, a_{t}\right)\right)\right] \] 其中 \(\mathbb{E}_{\pi} Q(x, \cdot) \equiv \sum_{a \in \mathcal{A}} \pi(a | x) Q(x, a)\) 。 \(\mathcal{R}^{\pi, \mu}\) 提供了常规的累积期望带有衰减的奖励和,但是轨迹中的每个奖励值都会有一个 off-policy 修正,这个修正我们定义为 \(Q\) 值的期望与 \(Q\) 值的差。 这个时候,\(Q^\pi\) 对于任何行为策略 \(\mu\) 来说即为 \(\mathcal{R}^{\pi, \mu}\) 最终收敛的不动点。
对于 n-step and -versions 的 \(\mathcal{R}^{\pi, \mu}\) ,定义为: \[ \begin{align*} \mathcal{R}_{\lambda}^{\pi, \mu} Q \stackrel{\mathrm{def}}{=} & A^{\lambda}\left[\mathcal{R}_{n}^{\pi, \mu}\right] \tag{2} \\ \left(\mathcal{R}_{n}^{\pi, \mu} Q\right)(x, a) \stackrel{\mathrm{def}}{=} & r(x, a)+\mathbb{E}_{\mu}\left[\sum_{t=1}^{n} \left(\gamma^{t}\left(r_{t}+\mathbb{E}_{\pi} Q\left(x_{t}, \cdot\right)-Q\left(x_{t}, a_{t}\right)\right) \right) + \gamma^{n+1} \mathbb{E}_{\pi} Q\left(x_{n+1} \cdot \cdot\right) \right] \end{align*} \] 其中定义操作 \(A^{\lambda}[f(n)] \stackrel{\operatorname{def}}{=}(1-\lambda) \sum_{n \geq 0} \lambda^{n} f(n)\) 即为常规的 TD(\(\lambda\)) 权重累加系数。
理论上的更新算法很简单: \[ Q_{k+1}=\mathcal{R}_{\lambda}^{\pi_{k}, \mu_{k}} Q_{k} \] \(\left(Q_{k}\right)_{k \in \mathbb{N}}\) 是一系列对于 \(Q^{\pi_{k}}\) 的估计,其中 \(\pi_k\) 是第 \(k\) 个临时的目标策略。
然而在实际操作过程中,我们可以将公式 (2) 改写成: \[ \begin{aligned} \mathcal{R}_{\lambda}^{\pi, \mu} Q(x, a) &=Q(x, a)+\mathbb{E}_{\mu}\left[\sum_{t \geq 0}(\lambda \gamma)^{t} \delta_{t}^{\pi}\right] \\ \delta_{t}^{\pi} &\stackrel{\text { def }}{=} r_{t}+\gamma \mathbb{E}_{\pi} Q\left(x_{t+1}, \cdot\right)-Q\left(x_{t}, a_{t}\right) \end{aligned} \] 其中 \(\delta_{t}^{\pi}\) 称为 expected TD-error。离线更新(需要等待一个完整的 episode 结束)的向前视角即为: \[ Q_{k+1}(x, a) \leftarrow Q_{k}(x, a)+\alpha_{k} \sum_{t=0}^{T_{k}}(\gamma \lambda)^{t} \delta_{t}^{\pi_{k}} \] 当然也可以使用在线更新的后向视角形式,这需要用到资格迹,论文中算法 (1) 即为这种更新模式。
论文在 Related Work 中与 SARSA(\(\lambda\)) 做了一下比较, SARSA(\(\lambda\)) 对 \(Q\) 的更新为: \[ Q_{s+1}\left(x_{s}, a_{s}\right) \leftarrow Q_{s}\left(x_{s}, a_{s}\right)+\alpha_{s}(A^{\lambda} R_{s}^{(n)}-Q\left(x_{s}, a_{s}\right)) \\ R_{s}^{(n)}=\sum_{t=s}^{s+n} \gamma^{t-s} r_{t}+\gamma^{n+1} Q\left(x_{s+n+1}, a_{s+n+1}\right) \] \(\Delta_s\) 为 \(t\) 时刻的更新总量,也可以像上文一样重写为 one-step TD-errors 的形式: \[ \begin{aligned} \Delta_{s} &=\sum_{t \geq s}(\lambda \gamma)^{t-s} \delta_{t} \\ \delta_{t} &=r_{t}+\gamma Q\left(x_{t+1}, a_{t+1}\right)-Q\left(x_{t}, a_{t}\right) \end{aligned} \] 该形式的推导过程与 GAE 非常相似。
论文最后比较了一下几个常见的 -return 算法,我们只列出比较重要的几个:
| 算法 | n-step 回报 | 更新规则 | 固定点 |
|---|---|---|---|
| TD() (on-policy) |
\(\sum_{t=s}^{s+n} \gamma^{t-s} r_{t}+\gamma^{n+1} V\left(x_{s+n+1}\right)\) | \(\sum_{t \geq s}(\lambda \gamma)^{t-s} \delta_{t}\) \(\delta_{t}=r_{t}+\gamma V\left(x_{t+1}\right)-V\left(x_{t}\right)\) |
\(V^{\mu}\) |
| SARSA() (on-policy) |
\(\sum_{t=s}^{s+n} \gamma^{t-s} r_{t}+\gamma^{n+1} Q\left(x_{s+n+1}, a_{s+n+1}\right)\) | \(\sum_{t \geq s}(\lambda \gamma)^{t-s} \delta_{t}\) \(\delta_{t}=r_{t}+\gamma Q\left(x_{t+1}, a_{t+1}\right)-Q\left(x_{t}, a_{t}\right)\) |
\(Q^{\mu}\) |
| Expected SARSA() (on-policy) |
\(\sum_{t=s}^{s+n} \gamma^{t-s} r_{t}+\gamma^{n+1} \mathbb{E}_{\mu} Q\left(x_{s+n+1}, \cdot\right)\) | \(\sum_{t \geq s}(\lambda \gamma)^{t-s} \delta_{t}+\mathbb{E}_{\mu} Q\left(x_{s}, \cdot\right)-Q\left(x_{s}, a_{s}\right)\) \(\delta_{t}=r_{t}+\gamma \mathbb{E}_{\mu} Q\left(x_{t+1}, \cdot\right)-\mathbb{E}_{\mu} Q\left(x_{t}, \cdot\right)\) |
\(Q^{\mu}\) |
| General Q() (off-policy) |
\(\sum_{t=s}^{s+n} \gamma^{t-s} r_{t}+\gamma^{n+1} \mathbb{E}_{\pi} Q\left(x_{s+n+1}, \cdot\right)\) | \(\sum_{t \geq s}(\lambda \gamma)^{t-s} \delta_{t}+\mathbb{E}_{\pi} Q\left(x_{s}, \cdot\right)-Q\left(x_{s}, a_{s}\right)\) \(\delta_{t}=r_{t}+\gamma \mathbb{E}_{\pi} Q\left(x_{t+1}, \cdot\right)-\mathbb{E}_{\pi} Q\left(x_{t}, \cdot\right)\) |
\(Q^{\mu, \pi}\) |
| \(Q^\pi(\lambda)\) (on/off-policy) |
\(\sum_{t=s}^{s+n} \gamma^{t-s}\left[r_{t}+\mathbb{E}_{\pi} Q\left(x_{t}, \cdot\right)-Q\left(x_{t}, a_{t}\right)\right]\) \(+\gamma^{n+1} \mathbb{E}_{\pi} Q\left(x_{s+n+1}, \cdot\right)\) |
\(\sum_{t \geq s}(\lambda \gamma)^{t-s} \delta_{t}\) \(\delta_{t}=r_{t}+\gamma \mathbb{E}_{\pi} Q\left(x_{t+1}, \cdot\right)-Q\left(x_{t}, a_{t}\right)\) |
\(Q^\pi\) |
通过 Expected SARSA() 与 \(Q^\pi(\lambda)\) 的对比可以看出,\(Q^\pi(\lambda)\) 只是多了对即时奖励的修正部分
Safe and efficient off-policy reinforcement learning: Retrace(\(\lambda\))
然而,\(Q^\pi (\lambda)\) 算法中的行为策略 \(\mu\) 与目标策略 \(\pi\) 不能差别太大(\(\|\pi-\mu\|_{1} \leq \frac{1-\gamma}{\lambda \gamma}\)),也就导致了 Q(\(\lambda\)) 并不“安全”。Retrace(\(\lambda\)) 在 Q(\(\lambda\)) 的基础上进行了改进,有三个有点:
- 低方差
- 安全,可以利用从任意的行为策略中生成的轨迹,而不需要去关心它到底有多 off-policyness
- 高效,可以高效地利用与目标策略接近的行为策略所产生的轨迹
在论文中,作者总结了一个通用的可以比较各种 return-based off-policy 算法的操作为: \[ \mathcal{R} Q(x, a) :=Q(x, a)+\mathbb{E}_{\mu}\left[\sum_{t \geq 0} \gamma^{t}\left(\prod_{s=1}^{t} c_{s}\right)\left(r_{t}+\gamma \mathbb{E}_{\pi} Q\left(x_{t+1}, \cdot\right)-Q\left(x_{t}, a_{t}\right)\right)\right] \] 对于重要性采样来说,\(c_{s}=\frac{\pi\left(a_{s} | x_{s}\right)}{\mu\left(a_{s} | x_{s}\right)}\) ,但会有非常大(甚至是无限)的方差;
对于 off-policy \(Q^\pi(\lambda)\) ,\(c_{s}=\lambda\) ,但必须满足 \(\|\pi-\mu\|_{1} \leq \frac{1-\gamma}{\lambda \gamma}\) 否则无法工作;
对于 TB(\(\lambda\)) ,\(c_s=\lambda \pi(a_s|x_s)\) ,但在当 \(\mu\) 与 \(\pi\) 比较接近的时候(即比较接近 on-policy 的时候),把 traces 给截断就不是很高效了;
对于 Retrace(\(\lambda\)) ,\(c_{s}=\lambda \min \left(1, \frac{\pi\left(a_{s} | x_{s}\right)}{\mu\left(a_{s} | x_{s}\right)}\right)\) ,它将重要性比率截断至 1 。
而 V-trace 和 Retrace(\(\lambda\)) 类似,只不过 Retrace(\(\lambda\)) 估计的是 \(Q\) 函数,这里估计的是 \(V\) 函数,因此叫 V-trace。
参考
Espeholt, L., Soyer, H., Munos, R., Simonyan, K., Mnih, V., Ward, T., ... & Legg, S. (2018). Impala: Scalable distributed deep-rl with importance weighted actor-learner architectures. arXiv preprint arXiv:1802.01561.
Harutyunyan, Anna, Marc G Bellemare, Tom Stepleton, and Remi Munos. “Q() with Off-Policy Corrections,” n.d., 15.
Munos, Remi, Tom Stepleton, Anna Harutyunyan, and Marc Bellemare. “Safe and Efficient Off-Policy Reinforcement Learning,” n.d., 9.
https://deepmind.com/blog/impala-scalable-distributed-deeprl-dmlab-30/

