卡耐基梅隆大学、加利福尼亚大学伯克利分校和 Google Brain 尝试了一种新的 Meta Learning 方法: Diversity is all you need: Learning skills without a reward function ,它能让智能体在没有外部奖励的情况下,通过最大熵策略来最大化一个信息论里的目标函数,以此学习到有用的技能 (skills) 。在一系列机器人模拟的任务中,智能体可以在无监督的情况下学习到各种技能,比如行走、跳。
Introduction
在深度强化学习中,智能体可以学习到很多由奖励函数驱动的技能 (reward-driven skills),但对于人类或者智慧生物来说,我们可以在环境中无监督地自行探索来学习一些有用的技能,而当我们面临一些特定的目标时,我们可以使用这些已经学习到的技能更快更好地完成这些目标。但这对于智能体来说,在没有奖励函数的情况下自动获取一些有用的技能是非常困难的。文中对技能 (skill) 做了如下定义:
A skill is a latent-conditioned policy that alters that state of the environment in a consistent way.
技能 是一种潜在的策略,它能以一致的方式来改变环境状况
我们假设,为了使智能体获取到的技能都是有用的,这些学习到的技能必须大到能覆盖一系列可能的行为模式。有可能某一种技能是无用的,比如随机游走 (random dithering) ,但其他技能必须与随机游走不同,以此来达到有用的效果。论文的一个关键思想是使用了一个判别器来区分不用的技能,并将这个判别器作为目标函数。
此外,技能的不同并不意味着技能的多样性 (diverse) ,可能状态中的一小点区别就能使技能不同,但在语义上并不能说他们符合多样性。为了解决这个问题,作者希望不仅要学习到不同的技能,还要学习尽可能多样的技能 (as diverse as possible) 。
该论文共有五个贡献:
- 提出了在没有奖励函数的情况下学习有用技能的方法
- 该方法可以在无监督下学习到各种多样的技能,比如跑、跳
- 这些学习到的技能可以用在分层强化学习中
- 这些学习到的技能可以很快地适应一个新的任务(迁移学习)
- 这些学习到的技能可以用在模仿强化学习中
本文主要介绍前两个贡献。
Diversity is All You Need
我们只考虑无监督的强化学习环境,智能体只能在有监督的环境中进行无监督的探索,以此学习到一些有用的技能来更容易地在有监督的环境中最大化具体任务的奖励。由于这些技能的学习过程中没有用到先验知识,所以这些技能可以被运用到许多不同的任务中。
How It Works
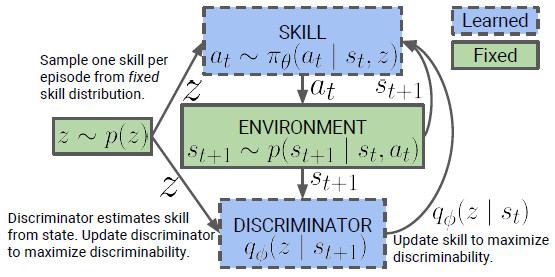
DIAYN ("Diversity is All You Need") 算法基于三个思想:
- 不同的技能应该访问到不同的状态,以此表现出技能之间的不同。
- 使用状态,而不是动作来表示技能的不同,因为不影响环境的动作对于外部观察者来说是不可见的,比如我们无法知道某个机器人用了多大力来推动一个茶杯如果这个茶杯没有动的话。
- 我们鼓励探索,尽可能刺激技能更加多样。拥有高方差,同时还能被判别器正确判别的技能必须要探索到某些其他技能没有探索到的状态空间,以免动作的随机性导致技能的多样但却不能被正确判别(与其他技能相同)。可见 1 和 3 是一对相互制约的关系。
论文中使用了信息论里的符号标记:\(S\) 和 \(A\) 为状态与动作的随机变量;\(Z \sim p(z)\) 为隐变量,决定着我们的条件策略;我们将给定一个固定 \(Z\) 的条件下的策略称之为技能;\(I(\cdot ; \cdot)\) 和 \(\mathcal{H}[\cdot]\) 为互信息与香农熵,都以 \(e\) 为底。根据以上三个思想,构造目标函数的三项:
- 在我们的目标函数中,我们最大化技能与状态的互信息 \(I(S ; Z)\) ,来表示技能应该控制智能体所访问的状态,同时,互信息也能表明我们可以从访问到的状态推断出当前的技能。
- 为了确保区别技能的是状态,而不是动作,在给定状态下,我们要最小化技能与动作的互信息 \(I(A ; Z | S)\) 。
- 把所有的技能结合 \(p(z)\) 视为所有的混合策略,我们要最大化这个混合策略的熵 \(\mathcal{H}[A | S]\) 。
结合以上三点,我们要最大化:
\[ \begin{align*} \mathcal{F}(\theta) & \triangleq I(S ; Z)+\mathcal{H}[A | S]-I(A ; Z | S) \tag{1} \\ &=(\mathcal{H}[Z]-\mathcal{H}[Z | S])+\mathcal{H}[A | S]-(\mathcal{H}[A | S]-\mathcal{H}[A | S, Z]) \\ &=\mathcal{H}[Z]-\mathcal{H}[Z | S]+\mathcal{H}[A | S, Z] \tag{2} \end{align*} \]
公式 (2) 重新编排了一下目标函数,三项的直观解释为:
- 第一项鼓励先验分布 \(p(z)\) 有高熵,我们将 \(p(z)\) 固定为均匀分布,以此来保证最大熵。
- 第二项表明从当前状态推断技能 \(z\) 应该是很容易的。
- 第三项表明每一个技能应该越随机越好。
由于我们没有办法整合所有的状态与技能来精确计算 \(p(z|s)\) ,所以我们用一个需要学习的判别器 \(q_{\phi}(z | s)\) 来估计后验。The IM Algorithm : A variational approach to Information Maximization 中 \[ I(\mathbf{x}, \mathbf{y}) \geq \underbrace{H(\mathbf{x})}_{\text { ‘‘entrop’’ }}+\underbrace{\langle\log q(\mathbf{x} | \mathbf{y})\rangle_{p(\mathbf{x}, \mathbf{y})}}_{\text { ‘‘energy’’ }} \stackrel{\mathrm{def}}{=} \tilde{I}(\mathbf{x}, \mathbf{y}) \] 证明了 Jensen 不等式保证了用 \(q_{\phi}(z | s)\) 来代替 \(p(z|s)\) 有一个目标函数 \(\mathcal{F}(\theta)\) 的 ELBO \(\mathcal{G}(\theta, \phi)\) \[ \begin{align*} \mathcal{F}(\theta) &=\mathcal{H}[A | S, Z]-\mathcal{H}[Z | S]+\mathcal{H}[Z] \\ &=\mathcal{H}[A | S, Z]+\mathbb{E}_{z \sim p(z), s \sim \pi(z)}[\log p(z | s)]-\mathbb{E}_{z \sim p(z)}[\log p(z)] \\ & \geq \mathcal{H}[A | S, Z]+\mathbb{E}_{z \sim p(z), s \sim \pi(z)}\left[\log q_{\phi}(z | s)-\log p(z)\right] \triangleq \mathcal{G}(\theta, \phi) \end{align*} \]
Implementation
论文使用了 SAC 算法来训练基于条件隐变量 \(z\) 的策略 \(\pi_{\theta}(a | s, z)\) 。SAC 算法本身就最大化策略的熵,也就是我们目标函数 \(\mathcal{G}\) 里的第一项。作者发现熵的正则化项 \(\alpha=0.1\) 时能更好的平衡探索与判别 (trade-off between exploration and discriminability) 。作者将最大化 \(\mathcal{G}\) 中的期望替换为任务的伪奖励值 (pseudo-reward) : \[ r_{z}(s, a) \triangleq \log q_{\phi}(z | s)-\log p(z) \] 作者将 \(p(z)\) 构造为一个分类分布 (categorical distribution) 。在无监督学习过程中,我们先在回合的一开始采样一个技能 \(z\sim p(z)\) ,并根据这个技能在整个回合中进行进行决策。当智能体访问到了某个状态是很容易被判别的时候获得奖励,同时判别器进行更新来更好地通过访问的状态推断技能 \(z\) 。
整个过程可以用下图表示:
算法为:

参考
Eysenbach, B., Gupta, A., Ibarz, J., & Levine, S. (2018). Diversity is all you need: Learning skills without a reward function. arXiv preprint arXiv:1802.06070.
https://stepneverstop.github.io/rl-rough-reading.html#DIAYN

