Reinforcement learning with deep energy-based policies 论文提出了一种能在连续状态行为空间下学习基于能量 (energy-based) 的方法,并且将这种方法运用在最大熵策略上,提出了 soft Q-learning 算法。该算法可以增加智能体的探索,并且可以在不同任务之间进行知识迁移。
绝大多数深度强化学习方法的思想是找到一个确定性的最优策略 (deterministic notion of optimality) ,尽管一些随即策略可以增加智能体的探索,但基本都是启发式的如加入随机噪声或初始化一个有着高熵的随即策略。但在某些情况下,我们更喜欢学习随机策略,它可以增加在有着不同目标任务中的探索性,也可以通过预训练获得不同的组合性。那么在哪些情况下随机策略实际上是最优策略呢?之前的研究表明,当我们考虑最优控制与概率推断时,随机策略可能是最佳的选择,也就是最大熵学习问题的解决方法。从直觉上来说,我们不仅仅是要捕捉到唯一的一个有着最小代价(最大累计期望回报)的确定性行为轨迹 (behavior),而是一系列的有着低代价的行为轨迹,也就是说我们想要去学习能用多种方法完成任务的策略。如果我们能学习到这样的一种随机策略,那当我们想要在此基础上进行微调以适应更明确的任务时,这种策略会是一个非常好的初始化策略(比如首先让机器人学习前进的所有方法,然后以该策略为初始化策略,分别学习跑步、跳跃等任务)。
然而先前的解决最大熵随机策略问题的研究都只能运用在非常小规模的空间问题上,那么怎么将最大熵策略搜索 (policy search) 算法扩展到任意的策略分布 (policy distribution) 上呢?论文作者借用了基于能量的模型 (energy-based model EBM) ,将随机策略看作是 EBM ,能量函数 (energy function) 为 "soft" Q-function 。
Preliminaries
Maximum Entropy Reinforcement Learning
我们的目标是要去学习一个策略 \(\pi(a_t|s_t)\) ,传统强化学习的学习目标为: \[ \newcommand{\E}{\mathbb{E}} \pi_\text{std}^*=\arg\max_\pi \sum_t\E_{(s_t,a_t)\sim\rho_\pi}[r(s_t,a_t)] \] 而最大熵 RL 在奖励项后面增加了一项策略熵,目的就是不仅要最大化每一时刻的奖励还要与每一时刻的策略熵值结合起来考虑,增加策略的不确定度。 \[ \pi_\text{MaxEnt}^*=\arg\max_\pi \sum_t\E_{(s_t,a_t)\sim\rho_\pi}[r(s_t,a_t)+\alpha\mathcal{H}(\pi(\cdot|s_t))] \tag{1} \]
Soft Value Functions and Energy-Based Models
传统的策略一般是单峰策略分布 (unimodal policy distribution)
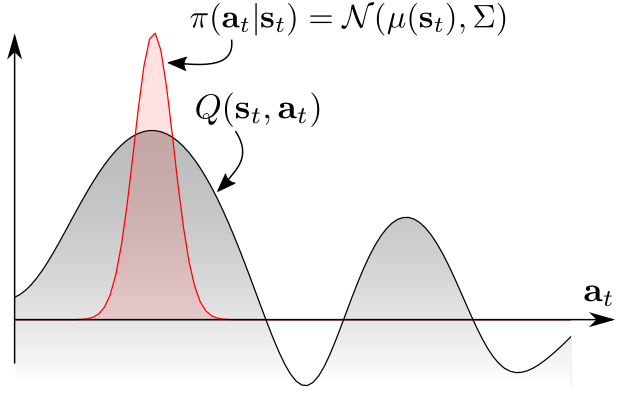
但根据图上的 Q 值分布,我们更希望采用多峰策略分布 (multimodal policy distribution)。
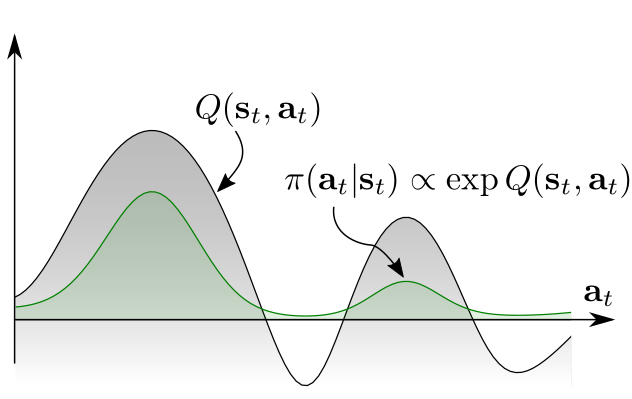
现在我们使用基于能量 (energy-based) 的策略来表示公式 (1) 中的随机策略 \(\pi\) : \[ \newcommand{\soft}{\text{soft}} \newcommand{\E}{\mathbb{E}} \pi(a_t|s_t) \propto \exp(-\mathcal{E}(s_t,a_t)) \] 其中 \(\mathcal{E}\) 就是能量函数 (energy function) ,可以用诸如深度神经网络来表示。论文中,作者将这个 energy function 与 soft 版本的 value function 和 Q function 结合起来,设置为 \(\mathcal{E}(s_t,a_t)=-\frac{1}{\alpha}Q_\soft(s_t,a_t)\) ,soft Q-function 定义为: \[ Q_\soft^*(s_t,a_t)=r_t+\E_{(s_{t+1,\cdots})\sim\rho _\pi}\left[ \sum_{l=1}^\infty \gamma^l(r_{t+l}+\alpha\mathcal{H}(\pi_{\text{MaxEnt}}^*(\cdot|s_{t+l}))) \right] \tag{2} \]
soft value function 定义为: \[ V_\soft^*(s_t)=\alpha\log\int_\mathcal{A} \exp\left( \frac{1}{\alpha}Q_\soft^*(s_t,a') \right) \mathrm{d}a' \] 此时最优策略为: \[ \begin{align*} \pi_\text{MaxEnt}^*(a_t|s_t)&=\exp\left(\frac{1}{\alpha}(Q_\soft^*(s_t,a_t)-V_\soft^*(s_t))\right) \tag{3} \\ &=\frac{\exp\left(\frac{1}{\alpha}Q_\soft^*(s_t,a_t)\right)}{\int_\mathcal{A} \exp\left( \frac{1}{\alpha}Q_\soft^*(s_t,a') \right) \mathrm{d}a'} \\ &=\frac{\exp\left(\frac{1}{\alpha}Q_\soft^*(s_t,a_t)\right)}{\exp\left(\frac{1}{\alpha}V_\soft^*(s_t)\right)} \end{align*} \] 可以看出 \(\frac{1}{\alpha}V_\soft(s_t)\) 为 log-partition function 。
公式 (2) 的 soft Q-function 满足 soft Bellman equation: \[ Q_\soft^*(s_t,a_t)=r_t+\gamma\E_{s_{t+1}\sim p_s}[V_\soft^*(s_{t+1})] \tag{4} \]
Soft Q-Learning
Soft Q-Iteration
与传统强化学习方法相同,我们用迭代的方法求解公式 (4) : \[ \begin{align*} Q_\soft(s_t,a_t) &\leftarrow r_t+\gamma\E_{s_{t+1}\sim p_s}[V_\soft(s_{t+1})] \\ V_\soft(s_t) &\leftarrow \alpha\log\int_\mathcal{A} \exp\left( \frac{1}{\alpha} Q_\soft(s_t,a') \right)\mathrm{d}a' \end{align*} \] 但这个迭代过程有非常大的问题,首先 soft Bellman backup 没有办法用在连续的状态行为空间上,其次没有办法根据公式 (3) 的策略进行采样,我们将在下文解决这些问题。
Soft Q-Learning
与 A Connection Between Generative Adversarial Networks, Inverse Reinforcement Learning, and Energy-Based Models 一文中用重要性采样的方法来估计 partition function 相同,这里也用到了重要性采样的方法来估计 soft value function,另外使用值函数近似的方法来估计以 \(\theta\) 为参数的 soft Q-function: \[ V_\soft^\theta(s_t) = \alpha\log \E_{q_{a'}}\left[ \frac{\exp\left( \frac{1}{\alpha} Q_\soft^\theta(s_t,a') \right)}{q_{a'}(a')} \right] \] 其中 \(q_{a'}\) 可以为任意的行为概率分布。损失函数为: \[ J_Q(\theta)=\E_{s_t\sim q_{s_t},a_t\sim q_{a_t}}\left[\frac{1}{2}\left( \hat{Q}_\soft^\overline{\theta}(s_t,a_t)-Q_\soft^\theta(s_t,a_t) \right)^2\right] \] 其中 \(\hat{Q}_\soft^\overline{\theta}(s_t,a_t)=r_t+\gamma\E_{s_{t+1}\sim p_s}[V_\soft^{\overline{\theta}}(s_{t+1})]\) 为 target Q-value,同时还要设置单独的 target network \(\overline{\theta}\) 。
然而,在连续空间中,我们仍然需要一个可行的方法从策略 \(\pi(a_t|s_t) \propto \exp\left(\frac{1}{\alpha}Q_\soft^\theta(s_t,a_t)\right)\) 中进行采样。
近似采样与 Stein Variational Gradient Descent (SVGD)
其实已经有许多从 energy-based distributiion 中采样的方法,比如 Markov chain Monte Carlo (MCMC) 方法,但在实际环境中,比如从策略中进行采样,用 MCMC 方法就不是很可行。作者使用了基于 SVGD 和 amortized SVGD 的采样网络。amortized SVGD 有许多优点,第一它提供了一个随机的采样网络,所以采样速度非常快,第二它最终会收敛到 EBM 的后验分布上,第三它可以与 actor-critic 算法联系起来。
我们希望学习一个与状态有关的随机神经网络 \(a_t=f^\phi(\xi;s_t)\) ,参数为 \(\phi\) ,能够将从高斯分布或任意分布而来的噪音样本 \(\xi\) 映射到来自于 EBM 的无偏行为样本。我们把这个策略记为 \(\pi^\phi(a_t|s_t)\) ,我们的目标是找到这个参数 \(\phi\) 使得这个估计的策略分布与真实的 energy-based distribution 策略的 KL 散度最小: \[ J_\pi(\phi;s_t)=D_{KL}\left( \pi^\phi(\cdot|s_t)\bigg\|\exp\left(\frac{1}{\alpha}(Q_\soft^\theta(s_t,\cdot)-V_\soft^\theta)\right) \right) \] 以下为 SVGD 中求解该损失函数梯度的过程。先计算 \[ \newcommand{\f}{f^\phi(\cdot;s_t)} \Delta \f=\E_{a_t\sim\pi^\phi}\Big[\kappa(a_t,\f)\nabla_{a'}Q_\soft^\theta(s_t,a')|_{a'=a_t}+\alpha\nabla_{a'}\kappa(a',\f)|_{a'=a_t}\Big] \] 其中 \(\kappa\) 为核函数(可以为高斯核函数)。根据 SVGD 的理论, \(\frac{\partial J_\pi}{\partial a_t}\propto \Delta f^\phi\) ,根据链式法则按如下梯度更新策略网络: \[ \frac{\partial J_\pi(\phi;s_t)}{\partial\phi}\propto\E_\xi\left[ \Delta f^\phi(\xi;s_t)\frac{\partial f^\phi(\xi;s_t)}{\partial\phi} \right] \] 可以发现,采样网络 \(f^\phi\) 实际上可以被看作是 actor-critic 中的 actor。具体算法如下:

参考
Haarnoja, T., Tang, H., Abbeel, P., & Levine, S. (2017). Reinforcement learning with deep energy-based policies. arXiv preprint arXiv:1702.08165.
https://bair.berkeley.edu/blog/2017/10/06/soft-q-learning/

