无模型预测 Model-Free Predication 一文中介绍了如何在没有模型的情况下,根据一个策略来评估该策略的价值函数,而这篇文章将在上文的基础上,来优化价值函数。
我们可以在无模型的情况下使用也可以在有模型但是模型太庞大只能用采样的方式来进行控制。
优化控制可以分为两类学习方式:
- 同策略学习 (On-policy learning) :我们需要优化一个策略 \(\pi\) ,就必须进行采样,而采样的方式就是根据要学习的策略 \(\pi\) 。该种学习方式称为同策略,即采样与学习的为同种策略。
- 异策略学习 (Off-policy learning) :同样是优化策略 \(\pi\) ,但采样时遵循的策略却是另一种策略 \(\mu\) ,相当于是根据前人已有的经验 \(\mu\) 来学习现有策略 \(\pi\) ,“站在巨人的肩膀上”。该种学习方式成为异策略,即采样与学习为不同的策略。
同策略蒙特卡罗控制 On-Policy Monte-Carlo Control
之前介绍过,在有模型的情况下使用动态规划方法的策略迭代算法,即先交替进行策略评估、策略改善,其中遵循贪婪策略的策略改善为: \[ \DeclareMathOperator*{\argmax}{arg\,max} \pi'(s) = \argmax_{a\in \mathcal{A}} \mathcal{R}^a_s + \mathcal{P}^a_{ss'}V(s') \] 但在无模型的情况下,我们无法知道某个状态的所有后续状态,也就无法知道下一步应该采用什么行为,所以我们使用行为价值函数来代替状态价值函数: \[ \pi'(s) = \argmax_{a\in\mathcal{A}}Q(s,a) \] 然而此时用贪婪策略的话,很有可能因为采样过少而产生一个局部最优解,比如现在有两扇门,首先打开左门获得奖励 0 ,再打开右门获得奖励 1 。此时根据贪婪策略,会一直打开右门,若打开右门得到的奖励都非负,那么就再也不会去去打开左门,但在这种情况下,是否打开右门就是最好的选择?为了解决这个问题,需要引入随机探索的机制,给其他行为一些机会被选择到,我们可以使用 ϵ-greedy 探索策略。
ϵ-Greedy Exploration
以 \(1-\epsilon\) 的概率选择最好的行为,以 \(\epsilon\) 的概率,在所有可能行为中随机选择(包括最好的行为): \[ \pi(a|s) = \begin{cases} \epsilon/m+1-\epsilon & \quad \text{if } a^* = \argmax_{a\in\mathcal{A}} Q(s,a) \\ \epsilon/m & \quad \text{otherwise} \end{cases} \] 可以证明在使用 ϵ-greedy 探索的情况下,\(v_{\pi'}(s) \ge v_\pi(s)\) ,即这个策略是在改善的。
此时的 MC 算法流程即为:
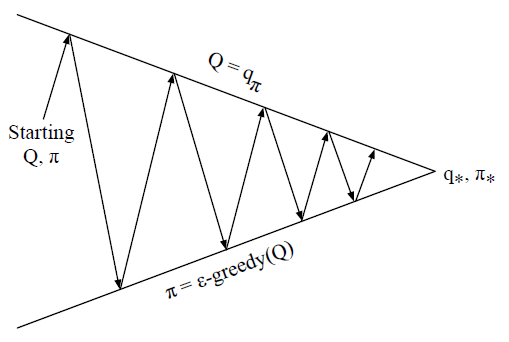
箭头向上为策略评估,向下为策略改善,使用的是 ϵ-greedy 方法。然而在策略评估阶段,理论上需要经历无限次回合才能收敛到 \(Q=q_\pi\) ,但实际上不需要经历那么久,我们可以每经历一个回合,就进行一次评估,近似到 \(Q \approx q_\pi\) ,同样整个 MC 算法仍会收敛:
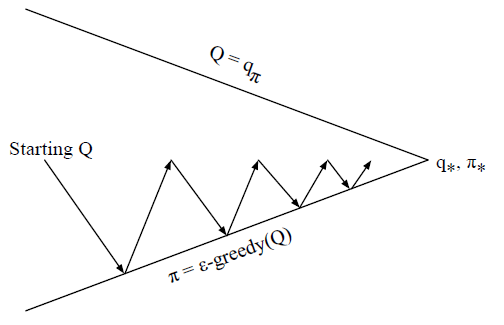
具体算法为:

GLIE (Greedy in the Limit with Infinite Exploration)
定义 GLIE 即为在有限的次数内进行无限的探索。要符合 GLIE 性必须符合两个条件:
- 所有的状态-行为对可以被探索无限次:\(\lim_{k \rightarrow \infty} N_k(s,a) = \infty\)
- 策略最终会收敛到贪婪策略上:\(\lim_{k\rightarrow\infty}\pi_k(a|s) = 1\{a=\argmax_{a'\in\mathcal{A}}Q_k(s,a')\}\)
举个例子,如果我们的 ϵ-greedy 为 \(\epsilon_k=\frac{1}{k}\) 那么\(\epsilon\) 最终会收敛到 0 上,也就满足了 GLIE 性。所以我们只需要根据策略 \(\pi\) 生成第 \(k\) 次回合序列 \(\{S_1,A_1,R_2,\cdots,S_T\} \sim \pi\) ,在该回合中对于每一个状态-行为对: \[ \begin{align*} N(S_t,A_t) &\leftarrow N(S_t,A_t)+1 \\ Q(S_t,A_t) &\leftarrow Q(S_t,A_t) + \frac{1}{N(S_t,A_t)} (G_t- Q(S_t,A_t)) \end{align*} \] 再进行策略改善: \[ \begin{align*} \epsilon &\leftarrow \frac{1}{k} \\ \pi &\leftarrow \epsilon\text{-greedy}(Q) \end{align*} \] 那么满足 GLIE 性的 MC 算法最终可以收敛到最优行为价值函数 \(Q(s,a) \rightarrow q_*(s,a)\)
同策略时间差分学习 On-Policy Temporal-Difference Learning
TD 与 MC 的区别在无模型预测中已经介绍过,参照上文,我们使用 TD 算法需要进行三个改进:
- 评估行为价值函数 \(Q(S, A)\)
- 使用 ϵ-greedy 进行策略改善
- 每探索一步就进行更新
Sarsa
用 Sarsa 来更新行为价值函数: \[ Q(S,A) \leftarrow Q(S,A) + \alpha (R+\gamma Q(S',A') - Q(S,A)) \] 很形象的可以表示为:在当前行为价值函数 \(Q(S,A)\) 下向前走一步获得即使 \(R\) 与下一步的行为价值函数 \(Q(S',A')\) ,连起来正好是 “SARSA” ,这也是 Sarsa 算法名字的来历。
具体算法为:

Sarsa(λ)
与 TD(λ) 相同,应用 Sarsa 算法也可以不仅仅只向前走一步,可以向前走 n 步,n-step Sarsa 为: \[ q_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1}R_{t+n} + \gamma^n Q(S_{t+n}) \\ Q(S,A) \leftarrow Q(S,A) + \alpha \left( q_t^{(n)} - Q(S,A) \right) \] 同样令 \(q^\lambda\) 将 n 步回报结合在一起,则 \[ q^\lambda_t = (1-\lambda) \sum^\infty_{n=1}\lambda^{n-1}q_t^{(n)} \] 那么前向视角的 Sarsa(λ) 为 \[ Q(S,A) \leftarrow Q(S,A) + \alpha \left( q_t^\lambda - Q(S,A) \right) \]
反向视角 Sarsa(λ)
与 TD(λ) 的反向视角相同,我们使用资格迹 (eligibility traces) 来进行在线更新 (online) ,但在 Sarsa(λ) 中,每一个状态-行为对就有一个资格迹,数量较多。 \[ \begin{align*} E_0(s,a) &=0\\ E_t(s,a) &= \gamma \lambda E_{t-1}(s,a) + 1\{S_t=s,A_t=a\} \end{align*} \] \[ \delta_t = R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)\\ Q(s,a) \leftarrow Q(s,a) + \alpha \delta_t E_t(s,a) \]
具体算法:

异策略学习 Off-Policy Learning
异策略即为计算价值函数或行为价值函数用来评估策略 \(\pi(a|s)\) 时,用另一种行为策略 \(\mu(a|s)\) 来采样: \[ \{S_1,A_1,R_2,\cdots,S_T\} \sim \mu \] 这样一来可以让我们从比如人类的经验或其他智能体的经验中进行学习,在学习最优策略的同时遵循探索性策略。
重要性采样 Importance Sampling
以一种不同的分布来估计期望: \[ \begin{align*} \mathbb{E}_{X\sim P}[f(X)] &= \sum P(X)f(X) \\ &= \sum Q(X) \frac{P(X)}{Q(X)} f(X) \\ &= \mathbb{E}_{X \sim Q} \left[ \frac{P(X)}{Q(X)} f(X) \right] \end{align*} \]
原来是随机变量根据概率密度 \(P\) 生成一系列的样本以此计算期望,现在根据概率密度 \(Q\) 生成样本再计算在该分布下的期望。
异策略蒙特卡罗
MC 中的回报由多次采样的奖励加权而成,运用异策略之后,回报也需要累乘重要性权重: \[ G_t^{\pi/\mu} = \frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}\frac{\pi(A_{t+1}|S_{t+1})}{\mu(A_{t+1}|S_{t+1})} \cdots \frac{\pi(A_T|S_T)}{\mu(A_T|S_T)} G_t \\ V(S_t) \leftarrow V(S_t) + \alpha \left( G_t^{\pi/\mu} - V(S_t) \right) \] 由于有分母存在,当 \(\pi\) 不为零时, \(\mu\) 不能为零。重要性采样可能会增加方差。
异策略时间差分
由于 TD(0) 只向前走了一步,所以只需要给 TD target 增加一个重要性权重即可: \[ V(S_t) \leftarrow V(S_t) + \alpha\left( \frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}(R_{t+1} + \gamma V(S_{t+1}))-V(S_t) \right) \]
Q-Learning
用异策略来学习行为价值函数 \(Q(s,a)\) ,不需要进行重要性采样,下一个行为的选择遵循行为策略 (behavior policy) \(A_{t+1} \sim \mu (\cdot|S_t)\),而另一种继任的行为的选择遵循目标策略 (target policy) \(A' \sim \pi (\cdot|S_t)\),以此得到更新过程: \[ Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha (R_{t+1} + \gamma Q(S_{t+1}, A') - Q(S_t, A_t)) \] 其中 target policy 对于 \(Q(s,a)\) 采用贪婪策略 \[ \pi(S_{t+1}) = \argmax_{a'} Q(S_{t+1},a') \] behavior pllicy对于 \(Q(s,a)\) 采用 ϵ-greddy 策略,所以 Q-Learning 的目标函数简化为: \[ \begin{align*} &R_{t+1} + \gamma Q(S_{t+1}, A') \\ =& R_{t+1} + \gamma Q(S_{t+1}, \argmax_{a'}Q(S_{t+1},a')) \\ =& R_{t+1} + \max_{a'}\gamma Q(S_{t+1},a') \end{align*} \]
所以 Q-Learning 控制算法为: \[ Q(S,A) \leftarrow Q(S,A) + \alpha \left( R + \gamma \max_{a'}Q(S', a') - Q(S,A) \right) \] 伪代码:
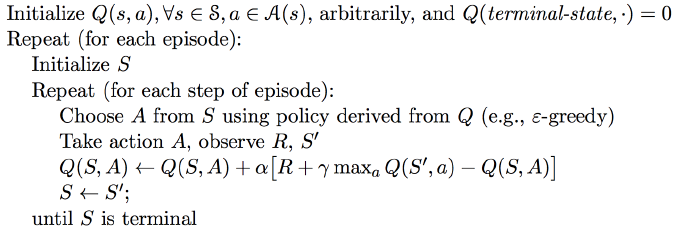
那为什么 Q-Learning 是异策略但不需要重要性采样呢?Quora 上有人给出了答案,我们可以看一下行为价值函数的贝尔曼最优方程: \[ Q(s,a) = R(s,a) + \gamma\sum_{s'}\mathcal{P_{ss'}^a} \max_{a'}Q(s',a') \] 其中 \(\mathcal{P_{ss'}^a}\) 是状态转移概率,而这里其实就是根据环境的状态转移概率分布来去求后一个状态最大的行为值函数的期望: \[ Q(s,a) = R(s,a) + \gamma \mathbb{E}_{s'\sim \mathcal{P_{ss'}^a}} \max_{a'}Q(s',a') \] 但贝尔曼方程的问题在于,现在的强化学习是无模型的,我们不知道状态转移概率是什么,但我们可以进行采样。回到 Q-Learning ,我们只是使用值迭代的方法,从任意的 \(Q\) 值开始,不断应用贝尔曼方程,但这时候我们不是用根据状态转移概率来计算期望值,而是直接从环境进行采样,使用估计的期望值。
所以,这里的重要性采样是根据环境的状态转移概率分布而来,不是策略分布,所以我们不需要用重要性采样来对另一个策略分布进行修正。
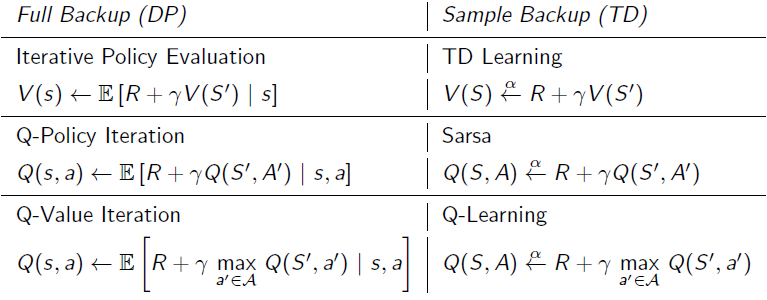
动态规划与时间差分的比较
参考
Sutton, R. S., & Barto, A. G. (1998). Reinforcement learning: An introduction (Vol. 1, No. 1). Cambridge: MIT press.
http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/control.pdf
https://zhuanlan.zhihu.com/p/28108498
https://www.quora.com/Why-doesn-t-DQN-use-importance-sampling-Dont-we-always-use-this-method-to-correct-the-sampling-error-produced-by-the-off-policy

