之前的所有方法都是基于值函数、行为价值函数,求出 \(V^\pi(s)\) 或 \(Q^\pi(s,a)\) 或是他们的近似函数来映射出最优策略。而基于策略的强化学习方法 (Policy-Based Reinforcement Learning) 则直接将策略参数化,即 \(\pi_\theta(s,a)=\mathbb{P}[a|s,\theta]\) ,利用参数化的线性、非线性函数来表示策略,寻找最优策略,而这个最优策略的搜索即是要将某个目标函数最大化。
Policy Gradient
策略目标函数 Policy Objective Functions
- Start Value :在能够产生完整 episode 的环境下,也就是说 agent 可以达到某个终止状态时,我们可以用 start value 来衡量策略的优劣,就是初始状态 \(s_1\) 的累计奖励:
\[ J_1(\theta) = V^{\pi_\theta}(s_1) = \mathbb{E}_{\pi_\theta}[v_1] \]
- Average Value :在连续环境下,我们可以使用各状态的价值函数平均值:
\[ J_{avV}(\theta) = \sum_s d^{\pi_\theta}(s) V^{\pi_\theta}(s) \]
- Average Reward per Time-Step :我们也可以使用每一时间步长下的平均奖励:
\[ J_{avR}(\theta) = \sum_s d^{\pi_\theta}(s) \sum_a \pi_\theta(s,a)\mathcal{R}_s^a \]
其中 \(d^{\pi_\theta}(s)=\sum_{s' \in \mathcal{S}} d^{\pi_\theta} (s') \mathcal{P}_{s's}\) 是基于策略 \(\pi_\theta\) 的状态的静态分布。
似然比 Likelihood Ratios
假设策略 \(\pi_\theta\) 是可导的且不等于0,则似然比 (Likelihood ratios) 为: \[ \begin{align*} \nabla_\theta \pi_\theta(s,a) &= \pi_\theta(s,a)\frac{\nabla_\theta \pi_\theta(s,a) }{\pi_\theta(s,a)} \\ &= \pi_\theta(s,a) \nabla_\theta \log\pi_\theta(s,a) \end{align*} \] 其中 \(\log\pi_\theta(s,a)\) 叫做 Score Function 。
对于离散动作,可以用 Softmax Policy: \[ \pi_\theta(s,a) = \frac{e^{\phi(s,a)^T \theta}}{\sum_{a'}e^{\phi(s,a')^T \theta}} \\ \nabla_\theta \log \pi_\theta(s,a) = \phi(s,a) - \mathbb{E}_{\pi_\theta} [\phi(s,\cdot)] \] 对于连续动作,可以用高斯策略 (Gaussian Policy) ,均值为 \(\mu(s) = \phi(s)^T\theta\) ,方差可以固定也可以参数化: \[ a \sim \mathcal{N}(\mu(s), \sigma^2) \\ \nabla_\theta \log \pi_\theta(s,a) = \frac{(a-\mu(s))\phi(s)}{\sigma^2} \] ## 策略梯度定理 Policy Gradient Theorem
先考虑一个非常简单的单步 (one-step) MDP 问题:初始状态 \(s \sim d(s)\) ,只经历一步得到一个即时奖励 \(r=\mathcal{R}_{s,a}\) 就终止。由于是单步 MDP ,所以三种目标函数都是一样的,我们用似然比来计算策略梯度: \[ \begin{align*} J(\theta) &= \mathbb{E}_{\pi_\theta}[r]\\ &= \sum_s d^{\pi_\theta}(s) \sum_a \pi_\theta(s,a)\mathcal{R}_s^a \\ \nabla_\theta J(\theta) &= \sum_s d(s) \sum_a \pi_\theta(s,a) \nabla_\theta \log\pi_\theta(s,a) \mathcal{R_{s,a}} \\ &= \mathbb{E}_{\pi_\theta}[ \nabla_\theta \log\pi_\theta(s,a) r] \end{align*} \] 如果是多步 (multi-step) MDP ,我们要用长时价值 \(Q^\pi(s,a)\) 来代替即时奖励 \(r\) ,并且有如下定理:对于 \(J=J_1,\ J_{avR},\ \frac{1}{1-\gamma}J_{avV}\) 策略梯度都有: \[ \nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[ \nabla_\theta \log\pi_\theta(s,a) Q^{\pi_\theta}(s,a)] \] 证明在 Sutton, Richard S., et al. "Policy gradient methods for reinforcement learning with function approximation." Advances in neural information processing systems. 2000. 这篇论文的附录中。
这样一来有了期望公式,就可以用蒙特卡罗采样的方法求出近似期望。用 \(v_t\) 作为 \(Q^{\pi_\theta}(s,a)\) 的无偏采样样本,则传统 REINFORCE 算法为:
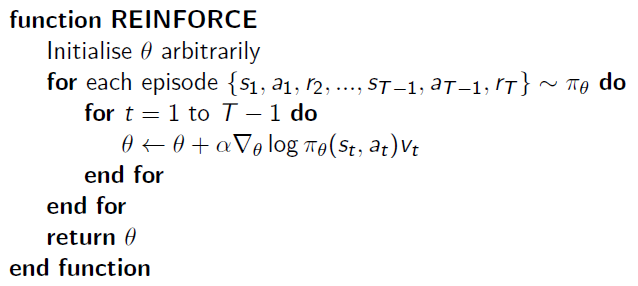
Actor-Critic 算法
蒙特卡罗策略梯度方法有着很高的方差,所以用一个 Critic 来估计行为价值函数 \(Q_w(s,a) \approx Q^{\pi_\theta}(s,a)\) 。所以 Actor-Critic 算法包含两种参数:
- Critic:更新行为价值函数的参数 \(w\)
- Actor:更新策略的参数 \(\theta\) ,更新过程会受到 Critic 的价值函数的引导
则用 Sasra 方法更新行为价值函数,用策略梯度更新 Actor 的算法为:

兼容近似函数 Compatible Function Approximation
由于要估计 Critic ,即是要最小化均方差: \[ \varepsilon=\mathbb{E}_{\pi_\theta}[( Q^{\pi_\theta}(s,a) - Q_w(s,a) )^2] \] 若达到了局部最优解,则: \[ \sum_s d^{\pi}(s) \sum_a \pi(s,a) [Q^\pi(s,a) - Q_w(s,a)] \nabla_w Q_w(s,a) = 0 \] 此时,如果: \[ \nabla_w Q_w(s,a) = \nabla_\theta \log \pi_\theta(s,a) \] 那么这时的策略梯度是准确的,即: \[ \nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[ \nabla_\theta \log\pi_\theta(s,a) Q_w(s,a)] \] 证明过程详见 Gradient Methods for Reinforcement Learning with Function Approximation 中的 Theorem 2 / Proof
但如果 \(\varepsilon=0\) 与 \(\nabla_w Q_w(s,a) = \nabla_\theta \log \pi_\theta(s,a)\) 都满足的话,整个算法也就相当于不使用 Critic ,变成了传统的REINFORCE 算法。
使用基准函数 (Baseline) 来减小方差
为了减小方差,引入基准函数 \(B(s)\) 与状态有关,与行为无关,可以使得 \(\mathbb{E}_{\pi_\theta}[ \nabla_\theta \log\pi_\theta(s,a) B(s)] = 0\)
而一个比较好的基准函数为状态价值函数 \(B(s) = V^{\pi_\theta}(s)\) ,所以可以将策略梯度修改一下,引入 Advantage Function:\(A^{\pi_\theta}(s,a)\) \[ A^{\pi_\theta}(s,a) = Q^{\pi_\theta}(s,a) - V^{\pi_\theta}(s) \\ \nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[ \nabla_\theta \log\pi_\theta(s,a) A^{\pi_\theta}(s,a)] \] 在这种情况下,需要两个近似函数也就是两套参数,一套用来近似状态价值函数,一套用来近似行为价值函数,以此来计算 Advantage Function 。然而在实际操作中,由于 TD 误差 \(\delta^{\pi_\theta} = r+\gamma V^{\pi_\theta}(s')-V^{\pi_\theta}(s)\) 是 Advantage Function 的无偏估计,即 \(\mathbb{E}_{\pi_\theta}[\delta^{\pi_\theta}|s,a] = A^{\pi_\theta}(s,a)\) ,所以可以直接用近似 TD 误差来计算策略梯度: \[ \delta_v= r+\gamma V_v(s')-V_v(s) \\ \nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[ \nabla_\theta \log\pi_\theta(s,a) \delta_v] \] 综上,在更新 Critic 时,可以用 MC, TD(0), forward-view TD(λ), backward-view TD(λ) ,同理在更新 Actor 时,也可以使用以上方法。
参考
Sutton R S. Policy Gradient Methods for Reinforcement Learning with Function Approximation[J]. Submitted to Advances in Neural Information Processing Systems, 1999, 12:1057-1063.
Silver D, Lever G, Heess N, et al. Deterministic policy gradient algorithms[C]// International Conference on International Conference on Machine Learning. JMLR.org, 2014:387-395.
http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/pg.pdf

